Question

Answer the following :

Find the lengths of the intercepts made on the co-ordinate axes, by the circle:

x² + y² – 8x + y – 20 = 0

Answer 1

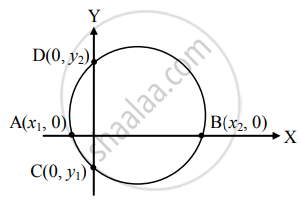
To find x-intercept made by the circle x² + y² + 2gx + 2fy + c = 0, substitute y = 0 and get a quadratic equation in x, whose roots are, say, x₁ and x₂.

These values represent the abscissae of ends A and B of x – intercept.

Length of x – intercept = |AB| = |x₂ – x₁| Similarly, substituting x = 0, we get a quadratic equation in y whose roots, say, y₁ and y₂ are ordinates of the ends C and D of y-intercept.

Length of y – intercept = |CD| = |y₂ – y₁|

Given equation of the circle is

x² + y² – 8x + y – 20 = 0      …(i)

Substituting y = 0 in (i), we get

x² – 8x – 20 = 0      …(ii)

Let AB represent the x-intercept, where

A = (x₁, 0), B = (x₂, 0)

x₁ + x₂ = 8 and x₁x₂ = – 20

(x₁ – x₂)² = (x₁ + x₂)² – 4 x₁x₂

= (8)² – 4(– 20)

= 64 + 80

= 144

∴ |x₁ – x₂| = `sqrt((x_1 + x_2)) = sqrt(144)` = 12

∴ Length of x – intercept = 12 units

Substituting x = 0 in (i), we get

y² + y – 20 = 0       …(iii)

Let CD represent the y – intercept, where

C = (0, y₁) and D = (0, y₂)

Then from (iii),

y₁ + y₂ = – 1 and y₁ y₂ = – 20

(y₁ – y₂)² = (y₁ + y₂)² – 4 y₁ y₂

= (– 1)² – 4(– 20)

= 1 + 80

= 81

∴ |y₁ – y₂| = `sqrt((y_1 - y_2)^2) = sqrt(81)` = 9

∴ Length of y – intercept = 9 units.

Answer 2

Given equation of the circle is

x² + y² – 8x + y – 20 = 0       …(i)

x-intercept:

Substituting y = 0 in (i), we get

x² – 8x – 20 = 0

∴ (x – 10)(x + 2) = 0

∴ x = 10 or x = –2

∴ length of x-intercept = |10 – (–2)| = 12 units

y-intercept:

Substituting x = 0 in (i), we get

y² + y – 20 = 0

∴ (y + 5)(y – 4) = 0

∴ y = –5 or y = 4

∴ length of y-intercept = |– 5 – 4| = 9 units