Advertisements
Advertisements
प्रश्न
Answer the following question.
Describe briefly the process of transferring the charge between the two plates of a parallel plate capacitor when connected to a battery. Derive an expression for the energy stored in a capacitor.
उत्तर
Consider a parallel plate capacitor which is connected across a battery. As soon as the charges from the battery reach one plate, due to insulating gap charge is not able to move further to the other plate. Thus, the positive charge is developed at one plate and a negative charge is developed on the other. As the amount of charge increases on the plates, a voltage is developed across the capacitor that is opposite to the applied voltage. Hence, the current flowing in the circuit decreases and gradually becomes zero. Thus, the charge is developed on the capacitor.
Energy Stored in a Charged Capacitor
The energy of a charged capacitor is measured by the total work done in charging the capacitor to a given potential.
Let us assume that initially, both the plates are uncharged. Now, we have to repeatedly remove small positive charges from one plate and transfer them to the other plate.
Let
q → Total quantity of charge transferred
V → Potential difference between the two plates
Then
q = CV
Now, when an additional small charge dq is transferred from the negative plate to the positive plate, the small work done is given by,
`dW = Vdq = q/C dq`
The total work is done in transferring charge Q is given by,
`W = ∫_0^Q q/C dq = 1/C∫_0^Q qdq = 1/C[q^2/2]_0^Q`
`W = Q^2/(2C)`
This work is stored as electrostatic potential energy U in the capacitor.
`U = Q^2/(2C)`
`U = (CV)^2/(2C) ...[∵ Q = CV]`
`U = 1/2 CV^2`
संबंधित प्रश्न
Explain briefly the process of charging a parallel plate capacitor when it is connected across a d.c. battery
In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10−3 m2 and the distance between the plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100 V supply, what is the charge on each plate of the capacitor?
Show that the force on each plate of a parallel plate capacitor has a magnitude equal to `(1/2)` QE, where Q is the charge on the capacitor, and E is the magnitude of the electric field between the plates. Explain the origin of the factor `1/2`.
A parallel plate capacitor is to be designed with a voltage rating 1 kV, using a material of dielectric constant 3 and dielectric strength about 107 Vm−1. (Dielectric strength is the maximum electric field a material can tolerate without breakdown, i.e., without starting to conduct electricity through partial ionisation.) For safety, we should like the field never to exceed, say 10% of the dielectric strength. What minimum area of the plates is required to have a capacitance of 50 pF?
A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness d/3, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor.
A parallel-plate capacitor is charged to a potential difference V by a dc source. The capacitor is then disconnected from the source. If the distance between the plates is doubled, state with reason how the following change:
(i) electric field between the plates
(ii) capacitance, and
(iii) energy stored in the capacitor
A parallel-plate capacitor with plate area 20 cm2 and plate separation 1.0 mm is connected to a battery. The resistance of the circuit is 10 kΩ. Find the time constant of the circuit.
Solve the following question.
A parallel plate capacitor is charged by a battery to a potential difference V. It is disconnected from the battery and then connected to another uncharged capacitor of the same capacitance. Calculate the ratio of the energy stored in the combination to the initial energy on the single capacitor.
A parallel plate capacitor is connected to a battery as shown in figure. Consider two situations:
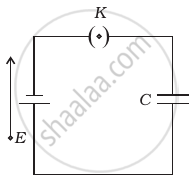
- Key K is kept closed and plates of capacitors are moved apart using insulating handle.
- Key K is opened and plates of capacitors are moved apart using insulating handle.
Choose the correct option(s).
- In A: Q remains same but C changes.
- In B: V remains same but C changes.
- In A: V remains same and hence Q changes.
- In B: Q remains same and hence V changes.
A parallel plate capacitor filled with a medium of dielectric constant 10, is connected across a battery and is charged. The dielectric slab is replaced by another slab of dielectric constant 15. Then the energy of capacitor will ______.
