Advertisements
Advertisements
प्रश्न
Answer the following question:
Find the equation of the line through the origin which bisects the portion of the line 3x + 2y = 2 intercepted between the co−ordinate axes.
उत्तर
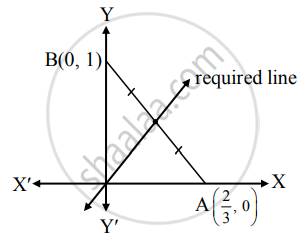
Given equation of the line is 3x + 2y = 2.
∴ `(3x)/2 + (2y)/2` = 1
∴ `x/(2/3) + y/1` = 1
This equation is of the form `x/"a" + y/"b"` = 1, with a = `2/3`, b = 1.
∴ The line 3x + 2y = 2 intersects the X-axis at A `(2/3, 0)` and Y-axis at B(0, 1).
The required line is passing through the midpoint of AB.
∴ Midpoint of AB = `((2/3 + 0)/2, (0 + 1)/2) = (1/3, 1/2)`
∴ Required line passes through (0, 0) and `(1/3, 1/2)`.
Equation of the line in two point form is
`(y - y_1)/(y_2 - y_1) = (x - x_1)/(x_2 - x_1)`
∴ The equation of the required line is
`(y - 0)/(1/2 - 0) = (x - 0)/(1/3 - 0)`
∴ 2y = 3x
∴ 3x – 2y = 0
APPEARS IN
संबंधित प्रश्न
Write the equation of the line :
parallel to the X−axis and at a distance of 5 unit form it and above it
Write the equation of the line :
parallel to the Y−axis and at a distance of 5 unit form it and to the left of it
Write the equation of the line :
parallel to the X-axis and at a distance of 4 unit form the point (−2, 3)
Obtain the equation of the line :
parallel to the Y−axis and making an intercept of 4 unit on the X−axis
Obtain the equation of the line containing the point :
A(2, – 3) and parallel to the Y−axis
Find the equation of the line passing through the points A(2, 0), and B(3, 4)
Find the equation of the line passing through the points P(2, 1) and Q(2, –1)
Find the equation of the line containing the origin and having inclination 60°
Find the equation of the line having slope `1/2` and containing the point (3, −2).
Find the equation of the line passing through the origin and which bisects the portion of the line 3x + y = 6 intercepted between the co-ordinate axes.
The vertices of a triangle are A(3, 4), B(2, 0), and C(−1, 6). Find the equation of the line containing side BC.
The vertices of a triangle are A(3, 4), B(2, 0), and C(−1, 6). Find the equation of the line containing the median AD
Find equations of altitudes of the triangle whose vertices are A(2, 5), B(6, –1) and C(–4, –3).
Find the equations of perpendicular bisectors of sides of the triangle whose vertices are P(−1, 8), Q(4, −2), and R(−5, −3)
Select the correct option from the given alternatives:
If the point (1, 1) lies on the line passing through the points (a, 0) and (0, b), then `1/"a" + 1/"b"` =
Select the correct option from the given alternatives:
The equation of the line through (1, 2), which makes equal intercepts on the axes, is
Select the correct option from the given alternatives:
If the line kx + 4y = 6 passes through the point of intersection of the two lines 2x + 3y = 4 and 3x + 4y = 5, then k =
Answer the following question:
Reduce the equation 6x + 3y + 8 = 0 into slope-intercept form. Hence find its slope
Answer the following question:
Does point A(2, 3) lie on the line 3x + 2y – 6 = 0? Give reason.
Answer the following question:
Find the equation of the line having slope 5 and containing point A(–1, 2).
Answer the following question:
The vertices of a triangle are A(1, 4), B(2, 3) and C(1, 6) Find equations of Perpendicular bisectors of sides
Answer the following question:
The vertices of a triangle are A(1, 4), B(2, 3) and C(1, 6) Find equations of altitudes of ∆ABC
Answer the following question:
Find the X−intercept of the line whose slope is 3 and which makes intercept 4 on the Y−axis
Answer the following question:
A(1, 4), B(2, 3) and C(1, 6) are vertices of ∆ABC. Find the equation of the altitude through B and hence find the co-ordinates of the point where this altitude cuts the side AC of ∆ABC.
Answer the following question:
Find the co-ordinates of the foot of the perpendicular drawn from the point P(−1, 3) the line 3x − 4y − 16 = 0
Answer the following question:
The perpendicular from the origin to a line meets it at (−2, 9). Find the equation of the line.
Answer the following question:
Show that there is only one line which passes through B(5, 5) and the sum of whose intercept is zero.
If the equation kxy + 5x + 3y + 2 = 0 represents a pair of lines, then k = ____________.
The slope of normal to the curve x = `sqrt"t"` and y = `"t" - 1/sqrt"t"`at t = 4 is _____.
The intercept of a line between the coordinate axes is divided by the point (1, 3) in the ratio 3 : 1. The equation of the line will be ______
Let the perpendiculars from any point on the line 7x + 56y = 0 upon 3x + 4y = 0 and 5x – 12y = 0 be p and p', then ______.
Area of the parallelogram formed by the lines y = mx, y = mx + 1, y = nx and y = nx + 1 is equal to ______.
N(3, – 4) is the foot of the perpendicular drawn from the origin to a line L. Then, the equation of the line L is ______.
