Advertisements
Advertisements
प्रश्न
Answer the following question in detail.
Derive an expression for the escape speed of an object from the surface of each.
उत्तर
- As the gravitational force due to Earth becomes zero at infinite distance, the object has to reach infinite distance in order to escape.
- Let us consider the kinetic and potential energies of an object thrown vertically upwards with escape velocity ve.
- On the surface of the Earth,
K.E. = `1/2 "mv"_"e"^2`
P.E. = `- "GMm"/"R"`
Total energy = P.E. + K.E.
∴ T.E. = `1/2"mv"_"e"^2 - "GMm"/"R"` ....(1) - The kinetic energy of the object will go on decreasing with time as it is pulled back by Earth’s gravitational force. It will become zero when it reaches infinity. Thus, at infinite distance from the Earth,
K.E. = 0
Also,
P.E. = `- "GMm"/∞` = 0
∴ Total energy = P.E. + K.E. = 0 - As energy is conserved
`1/2 "mv"_"e"^2 - "GMm"/"R" = 0` .....[From(1)]
or, `"v"_"e" = sqrt((2"GM")/"R")`
APPEARS IN
संबंधित प्रश्न
Define the escape velocity of a satellite.
Answer the following question.
On which factors does the escape speed of a body from the surface of Earth depend?
Answer the following question in detail.
Define escape speed.
Earth has mass M1 and radius R1. Moon has mass M2 and radius R2. Distance between their centre is r. A body of mass M is placed on the line joining them at a distance `"r"/3` from centre of the earth. To project the mass M to escape to infinity, the minimum speed required is ______.
A body is projected vertically from the surface of the earth of radius 'R' with velocity equal to half of the escape velocity. The maximum height reached by the body is ______.
The escape velocity from earth is 11.2 km. Another planet is having mass 1000 times and radius 10 times that of earth, then escape velocity at that planet will be ____________.
A hole is drilled half way to the centre of the earth. A body weighs 300 N on the surface of the earth. How much will, it weigh at the bottom of the hole?
A body is projected vertically upwards from earth's surface with velocity 2ve where ve is escape velocity from earth's surface. The velocity when body escapes the gravitational pull is ______.
What should be the velocity of earth due to rotation about its own axis so that the weight at equator becomes `(3/5)^"th"` of initial value?
(Radius of earth on equator = 6400 km, `g=10m/s^2,cos0^circ=1`)
A body is projected vertically upwards from earth's surface. If velocity of projection is `(1/3)^"rd"` of escape velocity, then the height upto which a body rises is ______.
(R =radius of earth)
A planet has radius `1/4`th of the radius of earth and acceleration due to gravity double than that of the earth. Then the ratio of escape velocity on the surface of planet to that on the earth's surface will be ______.
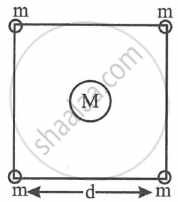
Four spheres each of mass m form a square of side d (as shown in figure). A fifth sphere of mass M is situated at the centre of square. The total gravitational potential energy of the system is ______.
A particle of mass M is situated at the centre of a spherical shell of same mass and radius a. The gravitational potential at a point situated at `"a"/2` distance from the centre, will be ______.
Two particles of masses m and 9m are separated by a distance r. At a point on the line joining them the gravitational field is zero. The gravitational potential at that point is ______.
( G = universal constant of gravitation)
The escape velocity on the surface of the earth is 11.2 kms-1. If mass and radius of a planet is 4 and 2 times of the earth respectively, then what is the escape velocity from the planet?
The ratio of the radii of the planets P1 and P2 is k. The ratio of acceleration due to gravity is r. The ratio of the escape velocities from them will be ______.
