Advertisements
Advertisements
प्रश्न
As shown figure, ∠DFE = 90°, FG ⊥ ED, if GD = 8, FG = 12, then EG = ?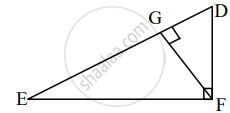
उत्तर
(i) In ∆DEF,
∠DFE = 90° and seg FG ⊥ hypotenuse ED ...[Given]
∴ FG2 = EG × GD ......[By theorem of geometric mean]
∴ (12)2 = EG × 8 ......[Given]
∴ 144 = EG × 8
∴ EG = `144/8`
∴ EG = 18 units
(ii) In ∆DGF,
∠DGF = 90° .....[ ⸪ FG ⊥ ED]
∴ FD2 = FG2 + GD2 ......[Pythagoras theorem]
∴ FD2 = (12)2 + (8)2 ......[Given]
∴ FD2 = 144 + 64
∴ FD2 = 208
∴ FD = `sqrt(16 xx 13)` ......[Taking square root of both sides]
∴ FD = `4sqrt(13)` units
(iii) In EGF,
∠EGF = 90° ......[⸪ FG ⊥ ED]
∴ EF2 = EG2 + FG2 ......[Pythagoras theorem]
∴ EF2 = (18)2 + (12)2 ......[From (i) and given]
∴ EF2 = 324 + 144
∴ EF2 = 468
∴ EF = `sqrt(36 xx 13)` .......[Taking square root of both sides]
∴ EF = `6sqrt(13)` units
APPEARS IN
संबंधित प्रश्न
In the given figure, ∠MNP = 90°, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
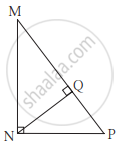
In the given figure, ∠QPR = 90°, seg PM ⊥ seg QR and Q–M–R, PM = 10, QM = 8, find QR.

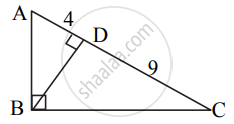
In right-angled ΔABC, BD ⊥ AC. If AD= 4, DC= 9, then find BD.
In the figure, ΔPQR is right angled at Q, seg QS ⊥ seg PR. Find x, y.

