Advertisements
Advertisements
प्रश्न
Bisect a straight angle, using ruler and compasses. Measure each part.
उत्तर
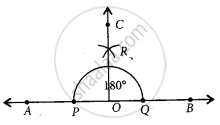
Steps of construction:
(i) Draw a line AB of any length.
(ii) Draw an arc of 180° which meets the ray `vec(OA)` at P and ray `vec(OB)` at Q.
(iii) Taking P and Q as centres and radius more than `1/2 (hat(PQ))`, draw two arcs which intersect each other at R.
(iv) Join OR and produce it to any point C.
(v) Thus, `vec(OC)` bisect the straight angle. Now, on measuring each angle we get, ∠BOC = ∠AOC = 90°.
APPEARS IN
संबंधित प्रश्न
Draw a line segment AB = 5.5 cm. Mark a point P, such that PA = 6 cm and PB = 4.8 cm. From point P, draw a perpendicular to AB.
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
8 cm
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
5.6 cm
Infinitely many perpendiculars can be drawn to a given ray.
In figure, the point C is the image of point A in line l and line segment BC intersects the line l at P.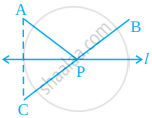
(a) Is the image of P in line l the point P itself?
(b) Is PA = PC?
(c) Is PA + PB = PC + PB?
(d) Is P that point on line l from which the sum of the distances of points A and B is minimum?
Copy figure on your notebook and draw a perpendicular from P to line m using (i) set squares (ii) protractor (iii) ruler and compass. How many such perpendicular are you able to draw?
Bisect ∠XYZ of figure.
Draw an angle of 60° using ruler and compasses and divide it into four equal parts. Measure each part.
Draw a line segment of length 6 cm. Construct its perpendicular bisector. Measure the two parts of theline segment.
Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?
