Advertisements
Advertisements
प्रश्न
Calculate the time period of a simple pendulum of length 1.44 m on the surface of the moon. The acceleration due to gravity on the surface of the moon is 1/6 the acceleration due to gravity on earth, [g = 9.8 ms−2]
उत्तर
Length of simple pendulum = l = 1.44 m
Time period (T) =?
Acceleration due to gravity on the surface of the moon
= g′ = `1/6xx"g"`
g = `9.8/6`
T = `2πsqrt(1/"g′")`
T = `2xx22/7xxsqrt((1.44xx6)/9.8)`
T = `14/7xx0.9389`
T = 5.90 s
APPEARS IN
संबंधित प्रश्न
The distance of a galaxy is 5·6 × 1025 m . Assuming the speed of light to be 3 × 108 `"ms"^-1`. Find the time taken by light to travel this distance .
[Hint : `"Time taken" = "Distance travelled"/"speed"`]
If the length of a simple pendulum is made one-fourth, then its time period becomes
The time period of a simple pendulum is 2 s. What is its frequency? What name is given to such a pendulum?
Which of the following do not affect the time period of a simple pendulum?
- mass of bob
- size of bob
- effective length of pendulum
- acceleration due to gravity
- amplitude.
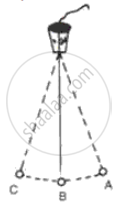
If a pendulum takes 0.5 s to travel from A to B as shown in the following figure, find its time period and frequency.