Advertisements
Advertisements
प्रश्न
Consider an ice cube of edge 1.0 cm kept in a gravity-free hall. Find the surface area of the water when the ice melts. Neglect the difference in densities of ice and water.
उत्तर
Given:
Edge of the ice cube (a) = 1.0 cm
The water that is formed due to the melting of ice acquires a spherical surface.
In the absence of gravity, let the radius of the spherical surface be r.
Volume of ice cube = volume of spherical surface of water
\[\Rightarrow a^3 = \frac{4}{3}\pi r^3 \]
\[ \Rightarrow r = \left[ \frac{3 a^3}{4\pi} \right]^{1/3}\]
Surface area of spherical water surface = 4πr2
\[= 4\pi \left[ \frac{3 a^3}{4\pi} \right]^{2/3} \]
\[ = \left( 36\pi \right)^{1/3} {\text{ cm }}^2\]
APPEARS IN
संबंधित प्रश्न
In a conical pendulum, a string of length 120 cm is fixed at rigid support and carries a mass
of 150 g at its free end. If the mass is revolved in a horizontal circle of radius 0.2 m around a
vertical axis, calculate tension in the string (g = 9.8 m/s2)
A 5.0 cm long straight piece of thread is kept on the surface of water. Find the force with which the surface on one side of the thread pulls it. Surface tension of water = 0.076 N m−1.
Two large glass plates are placed vertically and parallel to each other inside a tank of water with separation between the plates equal to 1 mm. Find the rise of water in the space between the plates. Surface tension of water = 0.075 Nm−1.
A metal piece of mass 160 g lies in equilibrium inside a glass of water. The piece touches the bottom of the glass at a small number of points. If the density of the metal is 8000 kg/m3, find the normal force exerted by the bottom of the glass on the metal piece.

A cube of ice floats partly in water and partly in K.oil (in the following figure). Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.

The energy stored in a soap bubble of diameter 6 cm and T = 0.04 N/m is nearly ______.
A u-tube is made up of capillaries of bore 1 mm and 2 mm respectively. The tube is held vertically and partially filled with a liquid of surface tension 49 dyne/cm and zero angles of contact. Calculate the density of the liquid, if the difference in the levels of the meniscus is 1.25 cm. take g = 980 cm/s2
The property of _______ of a liquid surface enables the water droplets to move upward in plants.
Define the surface tension of a liquid.
Distinguish between cohesive and adhesive forces.
Water rises in a capillary tube of radius r upto a height h. The mass of water in a capillary is m. The mass of water that will rise in a capillary of radius `"r"/4` will be ______.
Two spherical rain drops reach the surface of the earth with terminal velocities having ratio 16 : 9. The ratio of their surface area is ______.
A large number of liquid drops each of radius 'r' coalesce to form a big drop of radius 'R'. The energy released in the process in converted into kinetic energy of the big drop. The speed of the big drop is ______. (T = surface tension of liquid, p = density of liquid)
The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of the water column and 'h' is the height of water in the capillary. The inner circumference of the capillary is ______.
(surface tension of water = 7 × 10-2 N/m)
A coaxial cylinder made of glass is immersed in liquid of surface tension ' S'. Radius of inner and outer surface of cylinder are R1 and R2 respectively. Height till which liquid will rise is (Density of liquid is p):
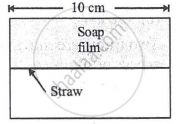
A soap film of surface tension 3 × 10-2 formed in a rectangular frame can support a straw as shown in Fig. If g = 10 ms-12, the mass of the straw is ______.
When one end of the capillary is dipped in water, the height of water column is 'h'. The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of water column. The inner circumference of capillary is ______.
(Surface tension of water = 7 × 10-2 N/m)
A liquid drop of density ρ is floating half immersed in a liquid of density d. The diameter of the liquid drop is ______.
(ρ > d, g = acceleration due to gravity, T = surface tension)
Define angle of contact.
