Advertisements
Advertisements
प्रश्न
Construct a ∆PQR in which QR = 5 cm, ∠P = 40° and the median PG from P to QR is 4.4 cm. Find the length of the altitude from P to QR.
उत्तर

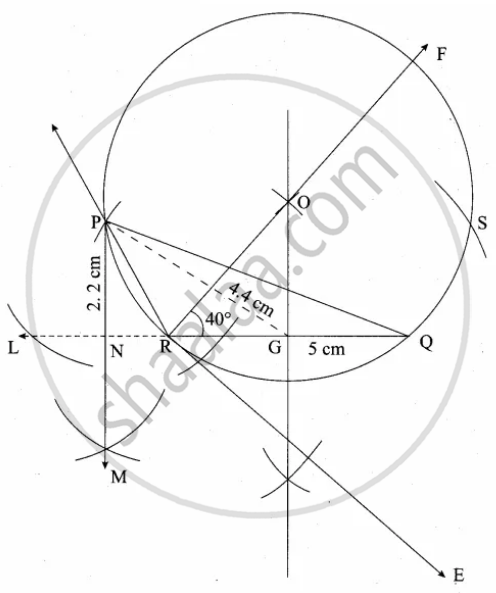
Steps of construction:
1. Draw a line segment RQ = 5 cm.
2. At R draw RE such that ∠QRE = 40°
3. At R, draw RF such that ∠ERF = 90°
4. Draw the perpendicular bisector to RQ, which intersects RF at O and RQ at G.
5. With O as centre and OP as radius draw a circle.
6. From G mark arcs of radius 4.4 cm on the circle. Mark them as P and S.
7. Join PR and PQ. Then ∆PQR is the required triangle.
8. From P draw a line PN which is perpendicular to RQ it meets at N.
9. Measure the altitude PN.
PN = 2.2 cm.
APPEARS IN
संबंधित प्रश्न
In ∆ABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB" = 3/4` and AC = 15 cm find AE
ABCD is a trapezium in which AB || DC and P, Q are points on AD and BC respectively, such that PQ || DC if PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD
Rhombus PQRB is inscribed in ΔABC such that ∠B is one of its angle. P, Q and R lie on AB, AC and BC respectively. If AB = 12 cm and BC = 6 cm, find the sides PQ, RB of the rhombus.
Check whether AD is bisector of ∠A of ∆ABC of the following
AB = 4 cm, AC = 6 cm, BD = 1.6 cm and CD = 2.4 cm.
∠QPR = 90°, PS is its bisector. If ST ⊥ PR, prove that ST × (PQ + PR) = PQ × PR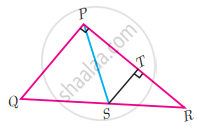
ABCD is a quadrilateral in which AB = AD, the bisector of ∠BAC and ∠CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD.
Draw a triangle ABC of base BC = 5.6 cm, ∠A = 40° and the bisector of ∠A meets BC at D such that CD = 4 cm
ST || QR, PS = 2 cm and SQ = 3 cm. Then the ratio of the area of ∆PQR to the area of ∆PST is
An Emu which is 8 feet tall is standing at the foot of a pillar which is 30 feet high. It walks away from the pillar. The shadow of the Emu falls beyond Emu. What is the relation between the length of the shadow and the distance from the Emu to the pillar?
Two circles intersect at A and B. From a point, P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.
