Advertisements
Advertisements
प्रश्न
ABCD is a quadrilateral in which AB = AD, the bisector of ∠BAC and ∠CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD.
उत्तर
ABCD is a quadrilateral. AB = AD.
AE and AF are the internal bisector of ∠BAC and ∠DAC
.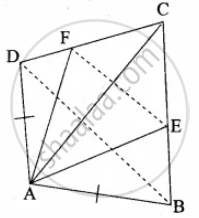
To prove: EF || BD.
Construction: Join EF and BD
Proof: In ∆ ABC, AE is the internal bisector of ∠BAC.
By Angle bisector theorem, we have,
∴ `"AB"/"AC" = "BE"/"EC"` ...(1)
In ∆ ADC, AF is the internal bisector of ∠DAC
By Angle bisector theorem, we have,
`"AD"/"AC"= "DF"/"FC"`
∴ `"AB"/"AC" = "DF"/"FC"` ...(AB = AD given) ...(2)
From (1) and (2), we get,
`"BE"/"EC" = "DF"/"FC"`
Hence in ∆ BCD,
BD || EF ...(by converse of BPT)
APPEARS IN
संबंधित प्रश्न
In ∆ABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB" = 3/4` and AC = 15 cm find AE
In ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm
If PQ || BC and PR || CD prove that `"AR"/"AD" = "AQ"/"AB"`
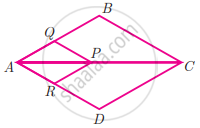
In trapezium ABCD, AB || DC, E and F are points on non-parallel sides AD and BC respectively, such that EF || AB. Show that = `"AE"/"ED" = "BF"/"FC"`
∠QPR = 90°, PS is its bisector. If ST ⊥ PR, prove that ST × (PQ + PR) = PQ × PR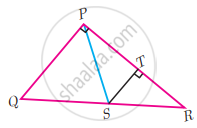
Construct a ∆PQR in which the base PQ = 4.5 cm, ∠R = 35° and the median from R to RG is 6 cm.
Construct a ∆ABC such that AB = 5.5 cm, ∠C = 25° and the altitude from C to AB is 4 cm
Draw a triangle ABC of base BC = 5.6 cm, ∠A = 40° and the bisector of ∠A meets BC at D such that CD = 4 cm
ABC is a triangle in which AB = AC. Points D and E are points on the side AB and AC respectively such that AD = AE. Show that the points B, C, E and D lie on a same circle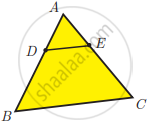
Two circles intersect at A and B. From a point, P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.
