Advertisements
Advertisements
प्रश्न
Construct a right-angled triangle in which: QP = QR and hypotenuse PR = 7 cm
उत्तर
In ΔPQR,
QP = QR ....(given)
⇒ ∠QPR = ∠QRP ....
Since hypotenuse PR = 7cm, ∠PQR = 90°
∴ ∠QPR + ∠QRP = 90°
⇒ ∠QPR = ∠QRP = 45°
Steps:
1. Draw PR = 7cm.
2. Draw a ray PT such as ∠RPT = 45° and ray RS such as ∠PRS = 45°
3. Ray RS and ray PT meets at Q.
Thus, PQR is the required triangle.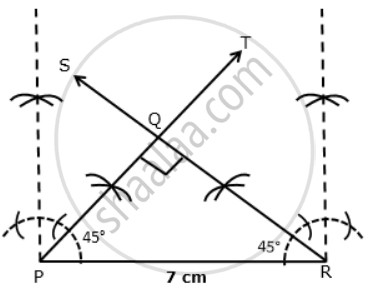
APPEARS IN
संबंधित प्रश्न
The perimeter of a triangle is 14.4 cm and the ratio of lengths of its side is 2 : 3 : 4. Construct the triangle.
In ΔABC, l(AB) = 5.5 cm, l(BC) = 4.2 cm, l(AC) = 3.5 cm
Draw an isosceles triangle with base 5 cm and the other sides 3.5 cm each.
Draw triangle with the measures given below.
In ∆ NTS, m ∠T = 40°, l(NT) = l(TS) = 5 cm
Draw triangle with the measures given below.
In ∆FUN, l(FU) = 5 cm, l(UN) = 4.6 cm, m∠U = 110°
Construct a triangle of the measures given below.
Construct a triangle of the measures given below.
In the right-angled ∆STU, hypotenuse SU = 5 cm and l(ST) = 4 cm.
Construct ∆XYZ such that l(XY) = 3.7 cm, l(YZ) = 7.7 cm, l(XZ) = 6.3 cm.
Construct an equilateral triangle using the given data: Altitude AD = 5 cm
Construct a ΔRST with side ST = 5.4 cm, RST = 60° and the perpendicular from R on ST = 3.0 cm.
