Advertisements
Advertisements
प्रश्न
Construct a triangle XYZ with the given conditions.
An equilateral triangle of side 7.5 cm
उत्तर
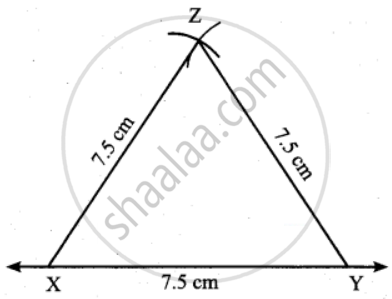
Construction:
Step 1: Drawn a line. Marked X and Y on the line such that XY = 7.5 cm.
Step 2: With X as centre, drawn an arc of radius 7.5 cm above the line XY.
Step 3: With Y as centre, drawn an arc of radius 7.5 cm to intersect arc drawn in steps.
Marked the point of intersection as Z.
Step 4: Joined XZ and YZ.
Now XYZ in the required triangle.
APPEARS IN
संबंधित प्रश्न
In Fig, AD = CD and AB = CB.
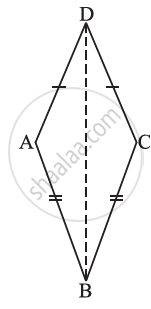
(i) State the three pairs of equal parts in ∆ABD and ∆CBD.
(ii) Is ∆ABD ≅ ∆CBD? Why or why not?
(iii) Does BD bisect ∠ABC? Give reasons.
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent: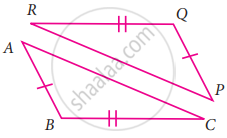
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent: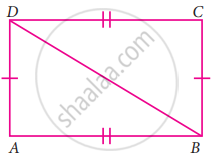
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent: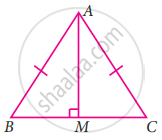
To conclude the congruency of triangles, mark the required information in the following figure with reference to the given congruency criterion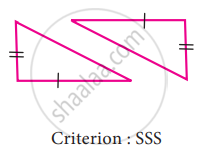
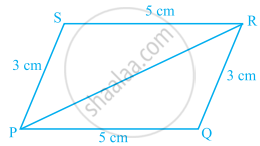
In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.

In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.
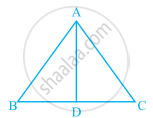
ABC is an isosceles triangle with AB = AC and D is the mid-point of base BC (see figure).
- State three pairs of equal parts in the triangles ABD and ACD.
- Is ∆ABD ≅ ∆ACD. If so why?
Triangles DEF and LMN are both isosceles with DE = DF and LM = LN, respectively. If DE = LM and EF = MN, then, are the two triangles congruent? Which condition do you use? If ∠E = 40°, what is the measure of ∠N?
If ΔPQR and ΔSOR are both isosceles triangle on a common base OR such that P and S lie on the same side of QR. Are triangles PSQ and PSR congruent? Which condition do you use?
