Advertisements
Advertisements
प्रश्न
Construct the following and give justification:
A triangle if its perimeter is 10.4 cm and two angles are 45° and 120°.
उत्तर
Step 1: Draw a line XY = 10.4 i.e., the perimeter.
Step 2: Construct an angle equal to ∠B = 45° and another angle equal to ∠C = 120°
Step 3: Bisect these angles and name the intersecting point as A.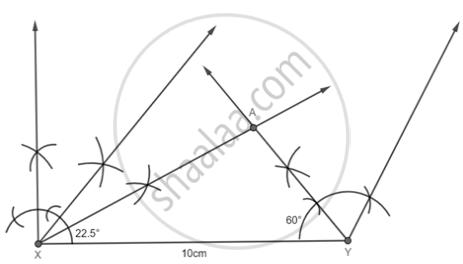
Step 4: Construct perpendicular bisectors of AX and AY and name the PQ and RS respectively.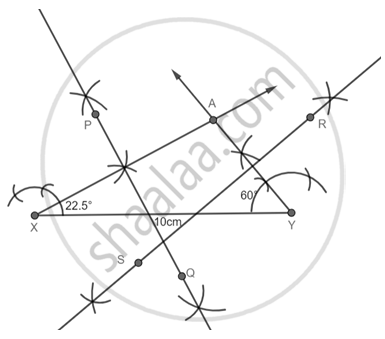
Step 5: Name the intersecting point of PQ and XY as B and RS the intersecting point of RS and XY as C.
Join AB and AC.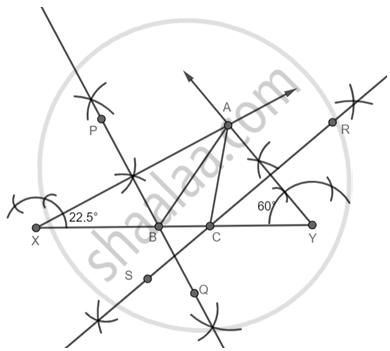
ABC is the required triangle.
Justification:
As B is on line PQ which is the perpendicular bisector of AX,
AB + BC + CA = XB + BC + CY = XY
Then, ∠BAX = ∠AXB ...(As in triangle AXB, AB is equal to XB)
As ∠ABC is the external angle of triangle AXB
Then, ∠ABC = ∠BAX + ∠AXB ...(Exterior angle sum property)
∠ABC = ∠AXB + ∠AXB
∠ABC = 2∠AXB = 45° or ∠B.
Similarly, ∠ACB = 2∠CAY = 120° or ∠C.
Thus the construction is justified.
APPEARS IN
संबंधित प्रश्न
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Construct the 75° angles and verify by measuring it by a protractor.
7. Draw a line segment AB and by ruler and compasses1 obtain a line segment of length `3/4`AB.
Draw an angle and label it as ∠BAC. Construct another angle, equal to ∠BAC.
Using protractor, draw a right angle. Bisect it to get an angle of measure 45°.
Construct the angle of the measurement:
1 . 75°
Construct the angle of the measurement:
1 . 105°
Construct the angle of the measurement:
1. 22 `(1°)/2`
Draw an angle of 80° with the help of a protractor. Then construct angles of (i) 40° (ii) 160° and (iii) 120°.
Construct a rhombus whose side is of length 3.4 cm and one of its angles is 45°.
