Advertisements
Advertisements
प्रश्न
Count the number of three-digit numbers which can be formed from the digits 2, 4, 6, 8 if repetitions of digits is allowed
उत्तर
Number of digits given = 4 (2, 4, 6, 8)
So the unit place can be filled in 4 ways,
10’s place can be filled in 4 ways and 100’s place can be filled in 4 ways
∴ The unit place, 10’s place and 100’s place together can be filled
(i.e) So the Number of 3 digit numbers = 4 × 4 × 4 = 64 ways
APPEARS IN
संबंधित प्रश्न
How many numbers between 100 and 1000 have the digit 7 exactly once?
A teacher wants to select the class monitor in a class of 30 boys and 20 girls. In how many ways can the monitor be selected if the monitor must be a girl or a boy?
A Signal is generated from 2 flags by putting one flag above the other. If 4 flags of different colours are available, how many different signals can be generated?
How many four digit numbers will not exceed 7432 if they are formed using the digits 2, 3, 4, 7 without repetition?
If numbers are formed using digits 2, 3, 4, 5, 6 without repetition, how many of them will exceed 400?
Select the correct answer from the given alternatives.
A college offers 5 courses in the morning and 3 in the evening. The number of ways a student can select exactly one course, either in the morning or in the evening
Select the correct answer from the given alternatives.
A college has 7 courses in the morning and 3 in the evening. The possible number of choices with the student if he wants to study one course in the morning and one in the evening is -
Three persons enter into a conference hall in which there are 10 seats. In how many ways they can take their seats?
In how many ways 5 persons can be seated in a row?
How many three-digit numbers, which are divisible by 5, can be formed using the digits 0, 1, 2, 3, 4, 5 if repetition of digits are not allowed?
How many strings can be formed using the letters of the word LOTUS if the word either starts with L or ends with S?
Count the total number of ways of answering 6 objective type questions, each question having 4 choices
Find the number of ways of distributing 12 distinct prizes to 10 students?
Find the value of 6!
Find the value of `(12!)/(9! xx 3!)`
Evaluate `("n"!)/("r"!("n" - "r")!)` when for any n with r = 2
Choose the correct alternative:
The number of 5 digit numbers all digits of which are odd i
How many numbers are there between 99 and 1000 having 7 in the units place?
In how many ways can this diagram be coloured subject to the following two conditions?
(i) Each of the smaller triangle is to be painted with one of three colours: red, blue or green.
(ii) No two adjacent regions have the same colour.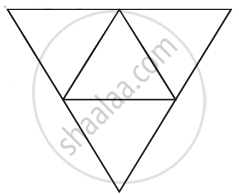
The number of possible outcomes when a coin is tossed 6 times is ______.
