Advertisements
Advertisements
प्रश्न
Four children are running a race:
In how many different ways could they finish the race?
उत्तर
The first and second places can be filled in 12 ways
The third-place can be filled (from the remaining 2 children) in 2 ways and the fourth place can be filled in 1 way
So the race can be finished in 12 × 2 × 1 = 24 ways
APPEARS IN
संबंधित प्रश्न
How many 4-letter code can be formed using the first 10 letters of the English alphabet, if no letter can be repeated?
A Signal is generated from 2 flags by putting one flag above the other. If 4 flags of different colours are available, how many different signals can be generated?
How many numbers formed with the digits 0, 1, 2, 5, 7, 8 will fall between 13 and 1000 if digits can be repeated?
A person went to a restaurant for dinner. In the menu card, the person saw 10 Indian and 7 Chinese food items. In how many ways the person can select either an Indian or a Chinese food?
A mobile phone has a passcode of 6 distinct digits. What is the maximum number of attempts one makes to retrieve the passcode?
Four children are running a race:
In how many ways can the first two places be filled?
Count the number of three-digit numbers which can be formed from the digits 2, 4, 6, 8 if repetitions of digits is allowed
How many three-digit numbers, which are divisible by 5, can be formed using the digits 0, 1, 2, 3, 4, 5 if repetition of digits are not allowed?
In how many ways 10 pigeons can be placed in 3 different pigeon holes?
Find the value of 3! – 2!
Find the value of `(12!)/(9! xx 3!)`
Find the value of n if (n + 1)! = 20(n − 1)!
Choose the correct alternative:
The number of ways in which the following prize be given to a class of 30 boys first and second in mathematics, first and second in physics, first in chemistry and first in English is
The number of ways in which a garland can be formed by using 10 identical pink flowers and 9 identical white flowers is ______
In how many ways can this diagram be coloured subject to the following two conditions?
(i) Each of the smaller triangle is to be painted with one of three colours: red, blue or green.
(ii) No two adjacent regions have the same colour.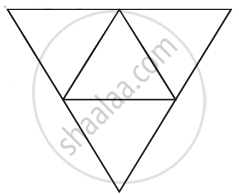
Eight chairs are numbered 1 to 8. Two women and 3 men wish to occupy one chair each. First the women choose the chairs from amongst the chairs 1 to 4 and then men select from the remaining chairs. Find the total number of possible arrangements.
Find the number of positive integers greater than 6000 and less than 7000 which are divisible by 5, provided that no digit is to be repeated.
