Advertisements
Advertisements
प्रश्न
Deduce the expression for the magnetic field at a point on the axis of a current carrying circular loop of radius ‘R’ distant ‘x’ from the centre. Hence, write the magnetic field at the centre of a loop.
उत्तर
dB∝ `(IDlxxr)/r^3`
`dB =mu_0/(4pi) (Idlxxr)/r^3`
Here, `mu_0/(4pi)`is a constant of proportionality.
The magnitude of this field is given as
`|dB|=mu_0/(4pi) (Idlsintheta)/r^2`
Magnetic field on the axis of a circular current loop:
Consider a circular loop carrying a steady current I. The loop is placed in the y–z plane
with its centre at origin O and has a radius R.

Let x be the distance of point P from the centre of the loop where the magnetic field is to
be calculated. Consider a conducting element dl of the loop. The magnitude dB of the
magnetic field due to dl is given by the Biot–Savart’s law as
`dB=mu_0/(4pi) (I|dlxxr|)/r^3`
From the figure, we see that r2 = x2 + R2.
Any element of the loop will be perpendicular to the displacement vector from the element to the axial point. Hence, we have `|dlxxr|=rdl` Thus, we have
`dB=mu_0/(4pi) (Idl)/r^2=mu_0/(4pi) (Idl)/(x^2+R^2) ".....(1)"`
The direction of dB is perpendicular to the plane formed by dl and r. It has an xcomponent
dBx and a component perpendicular to x-axis dB⊥
The perpendicular components cancel each other when summed over. Therefore, only the x component contributes. The net contribution is obtained by integrating dBx = dB cosθ
From the figure, we see that
`costheta=R/r=R/sqrt(x^2+R^2) "...(2)"`
From equations (1) and (2), we get
`dB_x=dBcostheta=mu_0/(4pi) (Idl)/(x^2+R^2)xxR/sqrt(x^2+R^2)=(mu_0Idl)/(4pi)xxR/(x^2+R^2)^(3/2)`
The summation of dl yields circumference of the loop 2πR. Hence, the magnetic field at
point P caused by the entire loop is
`B=B_xhati=(mu_0I(2piR))/(4pi)xxR/(x^2+R^2)^(3/2)hati`
`B=(mu_0IR^2)/(2(x^2+R^2)^(3/2))hati`
Case: At the centre of the loop
At the centre x = o, so we have
`B=(mu_0IR^2)/(2(R^2)^(3/2))hati=(mu_0IR^2)/(2R^3)hati=(mu_0I)/(2R)hati`
APPEARS IN
संबंधित प्रश्न
Use this law to find magnetic field due to straight infinite current carrying wire.
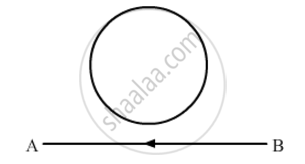
The electric current flowing in a wire in the direction from B to A is decreasing. Find out the direction of the induced current in the metallic loop kept above the wire as shown.
Explain the term hysteresis
The free electrons in a conducting wire are in constant thermal motion. If such a wire, carrying no current, is placed in a magnetic field, is there a magnetic force on each free electron? Is there a magnetic force on the wire?
A charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other. The particle will move in a ____________.
Correct unit of magnetic field is ______.
What is the magnetic induction of the field at the point O in a current I carrying wire that has the shape shown in the figure? The radius of the curved part of the wire is R, the linear parts are assumed to be very long.

In the product
`overset(->)("F") = "q"(overset(->)(υ) xx overset(->)("B"))`
= `"q"overset(->)(υ) xx ("B"overset(^)("i") + "B" overset(^)("j") + "B"_0overset(^)("k"))`
For q = 1 and `overset(->)(υ) = 2overset(^)("i") + 4overset(^)("j") + 6overset(^)("k")` and
`overset(->)("F") = 4overset(^)("i") - 20overset(^)("j") + 12overset(^)("k")`
What will be the complete expression for `overset(->)("B")`?
Two charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field B = B0k̂.
A beam of light travelling along X-axis is described by the electric field Ey = 900 sin ω(t - x/c). The ratio of electric force to magnetic force on a charge q moving along Y-axis with a speed of 3 × 107 ms-1 will be : [Given speed of light = 3 × 108 ms-1]
