Advertisements
Advertisements
Question
Deduce the expression for the magnetic field at a point on the axis of a current carrying circular loop of radius ‘R’ distant ‘x’ from the centre. Hence, write the magnetic field at the centre of a loop.
Solution
dB∝ `(IDlxxr)/r^3`
`dB =mu_0/(4pi) (Idlxxr)/r^3`
Here, `mu_0/(4pi)`is a constant of proportionality.
The magnitude of this field is given as
`|dB|=mu_0/(4pi) (Idlsintheta)/r^2`
Magnetic field on the axis of a circular current loop:
Consider a circular loop carrying a steady current I. The loop is placed in the y–z plane
with its centre at origin O and has a radius R.

Let x be the distance of point P from the centre of the loop where the magnetic field is to
be calculated. Consider a conducting element dl of the loop. The magnitude dB of the
magnetic field due to dl is given by the Biot–Savart’s law as
`dB=mu_0/(4pi) (I|dlxxr|)/r^3`
From the figure, we see that r2 = x2 + R2.
Any element of the loop will be perpendicular to the displacement vector from the element to the axial point. Hence, we have `|dlxxr|=rdl` Thus, we have
`dB=mu_0/(4pi) (Idl)/r^2=mu_0/(4pi) (Idl)/(x^2+R^2) ".....(1)"`
The direction of dB is perpendicular to the plane formed by dl and r. It has an xcomponent
dBx and a component perpendicular to x-axis dB⊥
The perpendicular components cancel each other when summed over. Therefore, only the x component contributes. The net contribution is obtained by integrating dBx = dB cosθ
From the figure, we see that
`costheta=R/r=R/sqrt(x^2+R^2) "...(2)"`
From equations (1) and (2), we get
`dB_x=dBcostheta=mu_0/(4pi) (Idl)/(x^2+R^2)xxR/sqrt(x^2+R^2)=(mu_0Idl)/(4pi)xxR/(x^2+R^2)^(3/2)`
The summation of dl yields circumference of the loop 2πR. Hence, the magnetic field at
point P caused by the entire loop is
`B=B_xhati=(mu_0I(2piR))/(4pi)xxR/(x^2+R^2)^(3/2)hati`
`B=(mu_0IR^2)/(2(x^2+R^2)^(3/2))hati`
Case: At the centre of the loop
At the centre x = o, so we have
`B=(mu_0IR^2)/(2(R^2)^(3/2))hati=(mu_0IR^2)/(2R^3)hati=(mu_0I)/(2R)hati`
APPEARS IN
RELATED QUESTIONS
Magnetic lines of force always cross each other
Which of the following particles will experience maximum magnetic force (magnitude) when projected with the same velocity perpendicular to a magnetic field?
An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path.
Which one of the following is a correct statement about magnetic forces?
In the product
`overset(->)("F") = "q"(overset(->)(υ) xx overset(->)("B"))`
= `"q"overset(->)(υ) xx ("B"overset(^)("i") + "B" overset(^)("j") + "B"_0overset(^)("k"))`
For q = 1 and `overset(->)(υ) = 2overset(^)("i") + 4overset(^)("j") + 6overset(^)("k")` and
`overset(->)("F") = 4overset(^)("i") - 20overset(^)("j") + 12overset(^)("k")`
What will be the complete expression for `overset(->)("B")`?
A charged particle of charge e and mass m is moving in an electric field E and magnetic field B. Construct dimensionless quantities and quantities of dimension [T]–1.
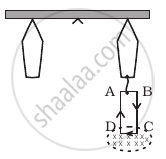
A 100 turn rectangular coil ABCD (in XY plane) is hung from one arm of a balance (Figure). A mass 500 g is added to the other arm to balance the weight of the coil. A current 4.9 A passes through the coil and a constant magnetic field of 0.2 T acting inward (in xz plane) is switched on such that only arm CD of length 1 cm lies in the field. How much additional mass ‘m’ must be added to regain the balance?
A beam of light travelling along X-axis is described by the electric field Ey = 900 sin ω(t - x/c). The ratio of electric force to magnetic force on a charge q moving along Y-axis with a speed of 3 × 107 ms-1 will be : [Given speed of light = 3 × 108 ms-1]
With a neat labelled diagram, explain cyclotron motion and cyclotron formula.
