Advertisements
Advertisements
Question
A charged particle of charge e and mass m is moving in an electric field E and magnetic field B. Construct dimensionless quantities and quantities of dimension [T]–1.
Solution
If a charged particle is moving in electric and magnetic field, we cannot construct any dimensionless quantity with these physical quantities.
For a charged particle moving perpendicular to the magnetic field, the magnetic Lorentz forces provide the necessary centripetal force for revolution.
Fm = qvB sin 90° = qvB ......(1)
We know that centripetal force = `(mv^2)/R` ......(2)
By equation (1) and (2)
`(mv^2)/R = qvB`
`v/R = (qB)/m`
∵ v = ωR and q = e
Angular velocity
ω = `v/R = (eB)/m`
Dimensional formula for angular velocity ω
ω = `[(eB)/m] = [v/R] = [T^-1]`
APPEARS IN
RELATED QUESTIONS
Obtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I
A charge ‘q’ moving along the X- axis with a velocity `vecv` is subjected to a uniform magnetic field B along the Z-axis as it crosses the origin O.
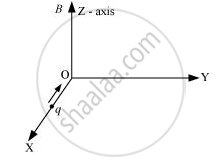
(i) Trace its trajectory.
(ii) Does the charge gain kinetic energy as it enters the magnetic field? Justify your answer.
The free electrons in a conducting wire are in constant thermal motion. If such a wire, carrying no current, is placed in a magnetic field, is there a magnetic force on each free electron? Is there a magnetic force on the wire?
Explain "Magnetic force never does any work on moving charges".
A solenoid 60 cm long and of radius 4.0 cm has 3 layers of windings of 300 turns each. A 2.0 cm long wire of mass 2.5 g lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of 6.0 A in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? (g = 9.8 m s–2)
A cubical region of space is filled with some uniform electric and magnetic fields. An electron enters the cube across one of its faces with velocity v and a positron enters via opposite face with velocity – v. At this instant ______.
- the electric forces on both the particles cause identical accelerations.
- the magnetic forces on both the particles cause equal accelerations.
- both particles gain or loose energy at the same rate.
- the motion of the centre of mass (CM) is determined by B alone.
At a certain place the angle of dip is 30° and the horizontal component of earth’s magnetic field is 0.5 G. The earth’s total magnetic field (in G), at that certain place, is ______.
Two conducting rails are connected to a source of emf and form an incline as shown in figure. A bar of mass 50 g slides without friction down the incline through a vertical magnetic field B. If the length of the bar is 50 cm and a current of 2.5 A is provided by battery. Value of B for which the bar slide at a constant velocity ______ × 10-1 Tesla. 2 [g = 10 m/s2]

Write the expression for the Lorentz force on a particle of charge q moving with a velocity `vecv` in a magnetic field `vecB`. When is the magnitude of this force maximum? Show that no work is done by this force on the particle during its motion from point `vecr_1` to point `vecr_2`.
