Advertisements
Advertisements
प्रश्न
A charged particle of charge e and mass m is moving in an electric field E and magnetic field B. Construct dimensionless quantities and quantities of dimension [T]–1.
उत्तर
If a charged particle is moving in electric and magnetic field, we cannot construct any dimensionless quantity with these physical quantities.
For a charged particle moving perpendicular to the magnetic field, the magnetic Lorentz forces provide the necessary centripetal force for revolution.
Fm = qvB sin 90° = qvB ......(1)
We know that centripetal force = `(mv^2)/R` ......(2)
By equation (1) and (2)
`(mv^2)/R = qvB`
`v/R = (qB)/m`
∵ v = ωR and q = e
Angular velocity
ω = `v/R = (eB)/m`
Dimensional formula for angular velocity ω
ω = `[(eB)/m] = [v/R] = [T^-1]`
APPEARS IN
संबंधित प्रश्न
Explain the term hysteresis
The net charge in a current-carrying wire is zero. Then, why does a magnetic field exert a force on it?
A straight horizontal wire of mass 10 mg and length 1.0 m carries a current of 2.0 A. What minimum magnetic field B should be applied in the region, so that the magnetic force on the wire may balance its weight?
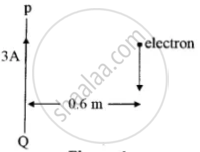
PQ is a long straight conductor carrying a current of 3A as shown in Figure below. An electron moves with a velocity of 2 x 107 ms-1 parallel to it. Find the force acting on the electron.
State whether the following statement is true or false:
Magnetic poles exist in pairs.
A charged particle is in motion having initial velocity `vecv` when it enters into a region of uniform magnetic field perpendicular to `vecv`. Because of the magnetic force the kinetic energy of the particle will ______.
A particle of charge -16 x 10-18 C moving with velocity 10 m/s along the X-axis enters a region where a magnetic field of induction B is along Y-axis and electric field of magnitude 104 V/m is along the negative Z-axis. If the charged particle continues moving along the X-axis, the magnitude of B is ____________.
A very high magnetic field is applied to a stationary charge. Then the charge experiences ______.
A cubical region of space is filled with some uniform electric and magnetic fields. An electron enters the cube across one of its faces with velocity v and a positron enters via opposite face with velocity – v. At this instant ______.
- the electric forces on both the particles cause identical accelerations.
- the magnetic forces on both the particles cause equal accelerations.
- both particles gain or loose energy at the same rate.
- the motion of the centre of mass (CM) is determined by B alone.
A circular coil of wire is made up of 200 turns, each of radius 10 cm. If a current of 0.5A passes through it, what will be the Magnetic field at the centre of the coil?
