Advertisements
Advertisements
प्रश्न
A cubical region of space is filled with some uniform electric and magnetic fields. An electron enters the cube across one of its faces with velocity v and a positron enters via opposite face with velocity – v. At this instant ______.
- the electric forces on both the particles cause identical accelerations.
- the magnetic forces on both the particles cause equal accelerations.
- both particles gain or loose energy at the same rate.
- the motion of the centre of mass (CM) is determined by B alone.
पर्याय
a, b and c
a, c and d
b, c and d
c and d
उत्तर
b, c and d
Explanation:
This problem is based upon the single moving charge placed with some uniform electric and magnetic fields in space. Then they experience a force called Lorentz force given by the relation Fnet = qE + q(v × B).
- The magnetic forces (Fm = q(v × B)), on charge particle is either zero or Fm is perpendicular to v (or component of v) which in turn revolves particles on a circular path with uniform speed. In both cases, particles have equal accelerations.
- Due to the same electric force (Fe = qE) which is in opposite direction (because of the sign of charge) both the particles gain or loss energy at the same rate.
- There is no change of the Centre of Mass (CM) of the particles, therefore the motion of the Centre of Mass (CM) is determined by B alone.
APPEARS IN
संबंधित प्रश्न
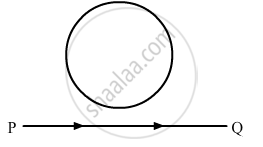
A conducting loop is held above a current carrying wire PQ as shown in the figure. Depict the direction of the current induced in the loop when the current in the wire PQ is constantly increasing.
A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil?
A steady current (I1) flows through a long straight wire. Another wire carrying steady current (I2) in the same direction is kept close and parallel to the first wire. Show with the help of a diagram how the magnetic field due to the current I1 exerts a magnetic force on the second wire. Write the expression for this force.
The net charge in a current-carrying wire is zero. Then, why does a magnetic field exert a force on it?
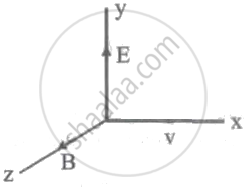
A particle with charge q moves with a velocity v in a direction perpendicular to the directions of uniform electric and magnetic fields, E and B respectively, which are mutually perpendicular to each other. Which one of the following gives the condition for which the particle moves undeflected in its original trajectory?
A solenoid 60 cm long and of radius 4.0 cm has 3 layers of windings of 300 turns each. A 2.0 cm long wire of mass 2.5 g lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of 6.0 A in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? (g = 9.8 m s–2)
In SI system, permeability has the units ______.
Which one of the following is a correct statement about magnetic forces?
The unit Wbm-2 is equal to ______.
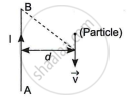
A long straight wire AB carries a current I. A particle (mass m and charge q) moves with a velocity `vec"v"`, parallel to the wire, at a distance d from it as shown in the figure. Obtain the expression for the force experienced by the particle and mention its directions.