Advertisements
Advertisements
प्रश्न
A cubical region of space is filled with some uniform electric and magnetic fields. An electron enters the cube across one of its faces with velocity v and a positron enters via opposite face with velocity – v. At this instant ______.
- the electric forces on both the particles cause identical accelerations.
- the magnetic forces on both the particles cause equal accelerations.
- both particles gain or loose energy at the same rate.
- the motion of the centre of mass (CM) is determined by B alone.
विकल्प
a, b and c
a, c and d
b, c and d
c and d
उत्तर
b, c and d
Explanation:
This problem is based upon the single moving charge placed with some uniform electric and magnetic fields in space. Then they experience a force called Lorentz force given by the relation Fnet = qE + q(v × B).
- The magnetic forces (Fm = q(v × B)), on charge particle is either zero or Fm is perpendicular to v (or component of v) which in turn revolves particles on a circular path with uniform speed. In both cases, particles have equal accelerations.
- Due to the same electric force (Fe = qE) which is in opposite direction (because of the sign of charge) both the particles gain or loss energy at the same rate.
- There is no change of the Centre of Mass (CM) of the particles, therefore the motion of the Centre of Mass (CM) is determined by B alone.
APPEARS IN
संबंधित प्रश्न
Two long, straight, parallel conductors carry steady currents, I1 and I2, separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other? Obtain the expression for this force. Hence, define one ampere.
The electric current flowing in a wire in the direction from B to A is decreasing. Find out the direction of the induced current in the metallic loop kept above the wire as shown.
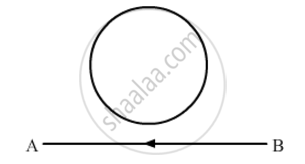
A long straight wire carries a current of 35 A. What is the magnitude of the field B at a point 20 cm from the wire?
A steady current (I1) flows through a long straight wire. Another wire carrying steady current (I2) in the same direction is kept close and parallel to the first wire. Show with the help of a diagram how the magnetic field due to the current I1 exerts a magnetic force on the second wire. Write the expression for this force.
An electron emitted by a heated cathode and accelerated through a potential difference of 2.0 kV, enters a region with uniform magnetic field of 0.15 T. Determine the trajectory of the electron if the field (a) is transverse to its initial velocity, (b) makes an angle of 30° with the initial velocity.
In the product `vec"F" = "q" (vec"υ" xx vec"B")`
= `"q" vec"υ" xx ("B"hat"i" +"B"hat"j" + "B"_0hat"k")`
For q = 1 and `vec"υ" = 2hat"i" + 4hat"j" + 6hat"k"` and
`vec"F" = 4hat"i" - 20hat"j" + 12hat"k"`
What will be the complete expression for `vec"B"`?
A charged particle would continue to move with a constant velocity in a region wherein ______.
- E = 0, B ≠ 0.
- E ≠ 0, B ≠ 0.
- E ≠ 0, B = 0.
- E = 0, B = 0.
Write the expression for the Lorentz force on a particle of charge q moving with a velocity `vecv` in a magnetic field `vecB`. When is the magnitude of this force maximum? Show that no work is done by this force on the particle during its motion from point `vecr_1` to point `vecr_2`.
State dimensions of magnetic field.
A circular coil of wire is made up of 200 turns, each of radius 10 cm. If a current of 0.5A passes through it, what will be the Magnetic field at the centre of the coil?
