Advertisements
Advertisements
प्रश्न
Write the expression for the Lorentz force on a particle of charge q moving with a velocity `vecv` in a magnetic field `vecB`. When is the magnitude of this force maximum? Show that no work is done by this force on the particle during its motion from point `vecr_1` to point `vecr_2`.
उत्तर
Lorentz force = Magnetic force + Electric force
⇒ `vecF = q(vecv xx vecB)`
`vecF = q.v.B sintheta`
when θ = 90° the Lorentz force is maximum.
If `vec(ds)` is the instantaneous displacement of charge and `vec(ds)` is also perpendicular to `vecF`.
Then,
W = `vecF. vec(ds)`
= `vecF vecs costheta`
= F.s cos90°
cos90° = 0
So, W = 0
Hence, no work is done by this force on the particle during its motion from a point `vecr_1` to point `vecr_2`.
संबंधित प्रश्न
Define magnetic lines of force
A circular coil of N turns and radius R carries a current I. It is unwound and rewound to make another coil of radius R/2, current I remaining the same. Calculate the ratio of the magnetic moments of the new coil and original coil.
A particle of charge ‘q’ and mass ‘m’ is moving with velocity .`vecV` It is subjected to a uniform magnetic field `vecB` directed perpendicular to its velocity. Show that it describes a circular path. Write the expression for its radius.
A charge ‘q’ moving along the X- axis with a velocity `vecv` is subjected to a uniform magnetic field B along the Z-axis as it crosses the origin O.
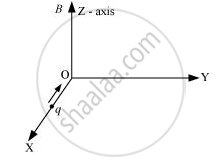
(i) Trace its trajectory.
(ii) Does the charge gain kinetic energy as it enters the magnetic field? Justify your answer.
A proton enters into a magnetic field of induction 1.732 T, with a velocity of 107 m/s at an angle 60° to the field. The force acting on the proton is e = 1.6 × 10-19 C, sin 60° = cos 30° = `sqrt3/2`
An electron emitted by a heated cathode and accelerated through a potential difference of 2.0 kV, enters a region with uniform magnetic field of 0.15 T. Determine the trajectory of the electron if the field (a) is transverse to its initial velocity, (b) makes an angle of 30° with the initial velocity.
A solenoid 60 cm long and of radius 4.0 cm has 3 layers of windings of 300 turns each. A 2.0 cm long wire of mass 2.5 g lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of 6.0 A in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? (g = 9.8 m s–2)
Show that a force that does no work must be a velocity dependent force.
An electron is moving along positive x-axis in a magnetic field which is parallel to the positive y-axis. In what direction will the magnetic force be acting on the electron?
State the expression for the Lorentz force on a charge due to an electric field as well as a magnetic field. Hence discuss the magnetic force on a charged particle which is (i) moving parallel to the magnetic field and (ii) stationary.
