Advertisements
Advertisements
प्रश्न
Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C ______.
- `oint B.dl = +- 2μ_0I`
- the value of `oint B.dl` is independent of sense of C.
- there may be a point on C where B and dl are perpendicular.
- B vanishes everywhere on C.
विकल्प
a and b
a and c
b and c
c and d
उत्तर
b and c
Explanation:
Ampere’s law gives another method to calculate the magnetic field due to a given current distribution.
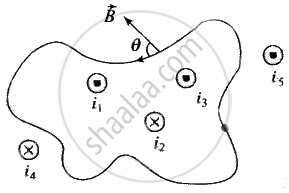
Line integral of the magnetic field `vecB` around any closed curve is equal to μ0 times the net current i threading through the area enclosed by the curve, i.e.
`oint vecB * vec(dl) = mu_0 sumi = mu_0 (i_1 + i_3 - i_2)`
Total current crossing the above area is `(i_1 + i_3 - i_2)`. Any current outside the area is not included in net current. (Outward ⊙ → + ve, Inward ⊗ → – ve)
Applying the Ampere's circuital law, we have
`ointB* dl = i_0 (I - I) = 0` (because current is in opposite sense)
Also, there may be a point on C where B and dl are perpendicular and hence, `oint_c B*dl = 0`
APPEARS IN
संबंधित प्रश्न
State Ampere’s circuital law.
Explain Ampere’s circuital law.
In Ampere's \[\oint \vec{B} \cdot d \vec{l} = \mu_0 i,\] the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
In order to have a current in a long wire, it should be connected to a battery or some such device. Can we obtain the magnetic due to a straight, long wire by using Ampere's law without mentioning this other part of the circuit?
In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero
(a) outside the cable
(b) inside the inner conductor
(c) inside the outer conductor
(d) in between the tow conductors.
A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
Using Ampere's circuital law, obtain an expression for the magnetic flux density 'B' at a point 'X' at a perpendicular distance 'r' from a long current-carrying conductor.
(Statement of the law is not required).
A thick current carrying cable of radius ‘R’ carries current ‘I’ uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance ‘r’ from the axis of the cable is represented by ______
Briefly explain various ways to increase the strength of the magnetic field produced by a given solenoid.
Using Ampere’s circuital law, obtain an expression for magnetic flux density ‘B’ at a point near an infinitely long and straight conductor, carrying a current I.
