Advertisements
Advertisements
प्रश्न
In order to have a current in a long wire, it should be connected to a battery or some such device. Can we obtain the magnetic due to a straight, long wire by using Ampere's law without mentioning this other part of the circuit?
उत्तर
We can obtain a magnetic field due to a straight, long wire using Ampere's law by mentioning the current flowing in the wire, without emphasising on the source of the current in the wire. To apply Ampere's circuital law, we need to have a constant current flowing in the wire, irrespective of its source.
APPEARS IN
संबंधित प्रश्न
State Ampere’s circuital law.
Electron drift speed is estimated to be of the order of mm s−1. Yet large current of the order of few amperes can be set up in the wire. Explain briefly.
Explain Ampere’s circuital law.
In Ampere's \[\oint \vec{B} \cdot d \vec{l} = \mu_0 i,\] the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
Consider the situation described in the previous problem. Suppose the current i enters the loop at the points A and leaves it at the point B. Find the magnetic field at the centre of the loop.
A thin but long, hollow, cylindrical tube of radius r carries i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
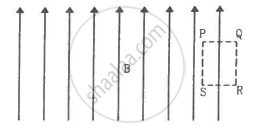
Sometimes we show an idealised magnetic field which is uniform in a given region and falls to zero abruptly. One such field is represented in figure. Using Ampere's law over the path PQRS, show that such a field is not possible.
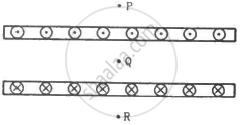
Two large metal sheets carry currents as shown in figure. The current through a strip of width dl is Kdl where K is a constant. Find the magnetic field at the points P, Q and R.
What is magnetic permeability?
State Ampere’s circuital law.
A straight wire of diameter 0.5 mm carrying a current of 1 A is replaced by another wire of 1 mm diameter carrying the same current. The strength of the magnetic field far away is ______.
Ampere's circuital law is used to find out ______
A thick current carrying cable of radius ‘R’ carries current ‘I’ uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance ‘r’ from the axis of the cable is represented by ______
Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C ______.
- `oint B.dl = +- 2μ_0I`
- the value of `oint B.dl` is independent of sense of C.
- there may be a point on C where B and dl are perpendicular.
- B vanishes everywhere on C.
Two concentric and coplanar circular loops P and Q have their radii in the ratio 2:3. Loop Q carries a current 9 A in the anticlockwise direction. For the magnetic field to be zero at the common centre, loop P must carry ______.
Read the following paragraph and answer the questions.
|
Consider the experimental set-up shown in the figure. This jumping ring experiment is an outstanding demonstration of some simple laws of Physics. A conducting non-magnetic ring is placed over the vertical core of a solenoid. When current is passed through the solenoid, the ring is thrown off. |
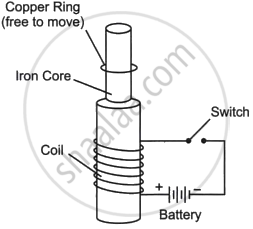
- Explain the reason for the jumping of the ring when the switch is closed in the circuit.
- What will happen if the terminals of the battery are reversed and the switch is closed? Explain.
- Explain the two laws that help us understand this phenomenon.
Using Ampere’s circuital law, obtain an expression for magnetic flux density ‘B’ at a point near an infinitely long and straight conductor, carrying a current I.
