Advertisements
Advertisements
प्रश्न
Consider the situation described in the previous problem. Suppose the current i enters the loop at the points A and leaves it at the point B. Find the magnetic field at the centre of the loop.
उत्तर
The loop ABCD can be considered as a circuit with two resistances in parallel, one along branch AB and other along branch ADC.
As, the sides of the loop are identical, their resistances are also same.
Let the resistance of each side be r.
The resistance of branch AB = r
The resistance of branch ADC = 3r
The current in the branches are calculated as:
As current follow the least resistive path so
Current in branch AB = \[\frac{3i}{4}\]
Current in branch ADC = \[\frac{i}{4}\]
At the centre of the loop:
Magnetic field due to wire AD, DC and CB will be into the plane of paper according to right hand thumb rule.
Magnetic field due to wire AB will be out of the plane of paper according to right hand thumb rule.
Net magnetic field at the centre = BAD +BDC +BCB − BAB which will be out of the plane of paper.
As, perpendicular distance of the centre from every wire will be equal to \[\frac{a}{\sqrt{2}}\] and angle made by corner points of each side at the centre is \[45^\circ \] .
\[B_{AD} = \frac{\mu_0 (\frac{i}{4})}{4\pi(\frac{a}{\sqrt{2}})}(\sin45^\circ + \sin45^\circ )\]
\[ = \frac{\mu_0 i}{8\pi a}\]
\[ B_{AD} = B_{DC} = B_{CB} \]
\[ B_{AD} + B_{DC} + B_{CB} = B^, = \frac{3 \mu_0 i}{8\pi a}\]
\[ B_{AB} = \frac{\mu_0 (\frac{3i}{4})}{4\pi(\frac{a}{\sqrt{2}})}(\sin45^\circ + \sin45^\circ )\]
\[ = \frac{3 \mu_0 i}{8\pi a}\]
\[ B_{net} = B^, - B_{AB} \]
\[ = 0\]
APPEARS IN
संबंधित प्रश्न
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
Using Ampere’s circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis ?
In Ampere's \[\oint \vec{B} \cdot d \vec{l} = \mu_0 i,\] the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
A long, straight wire carries a current. Is Ampere's law valid for a loop that does not enclose the wire, or that encloses the wire but is not circular?
A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
Consider the situation of the previous problem. A particle having charge q and mass mis projected from the point Q in a direction going into the plane of the diagram. It is found to describe a circle of radius r between the two plates. Find the speed of the charged particle.
Using Ampere's circuital law, obtain an expression for the magnetic flux density 'B' at a point 'X' at a perpendicular distance 'r' from a long current-carrying conductor.
(Statement of the law is not required).
State Ampere’s circuital law.
Define ampere.
Calculate the magnetic field inside and outside of the long solenoid using Ampere’s circuital law
Two identical current carrying coaxial loops, carry current I in opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C, then which statement is correct?
In a capillary tube, the water rises by 1.2 mm. The height of water that will rise in another capillary tube having half the radius of the first is:
A solenoid of length 0.6 m has a radius of 2 cm and is made up of 600 turns If it carries a current of 4 A, then the magnitude of the magnetic field inside the solenoid is:
Ampere's circuital law is used to find out ______
Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C ______.
- `oint B.dl = +- 2μ_0I`
- the value of `oint B.dl` is independent of sense of C.
- there may be a point on C where B and dl are perpendicular.
- B vanishes everywhere on C.
Read the following paragraph and answer the questions.
|
Consider the experimental set-up shown in the figure. This jumping ring experiment is an outstanding demonstration of some simple laws of Physics. A conducting non-magnetic ring is placed over the vertical core of a solenoid. When current is passed through the solenoid, the ring is thrown off. |
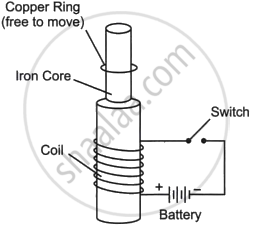
- Explain the reason for the jumping of the ring when the switch is closed in the circuit.
- What will happen if the terminals of the battery are reversed and the switch is closed? Explain.
- Explain the two laws that help us understand this phenomenon.
When current flowing through a solenoid decreases from 5A to 0 in 20 milliseconds, an emf of 500V is induced in it.
- What is this phenomenon called?
- Calculate coefficient of self-inductance of the solenoid.
