Advertisements
Advertisements
प्रश्न
Using Ampere’s circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis ?
उत्तर
Solenoid
• It consists of an insulating long wire closely wound in the form of helix.
• Its length is large as compared to its diameter.
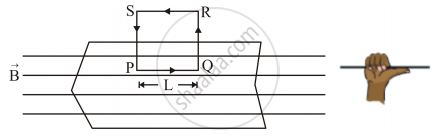
• Magnetic field due to RQ and SP path is zero because they are perpendicular to the axis of solenoid. Since SR is outside the solenoid, the magnetic field is zero.
• The line integral of magnetic field induction `vecB` over the closed path PQRS is
`oint_(PQRS) vecB*vecdl =oint_(PQ)vecB*vecdl =BL`
From Ampere’s circuital law,
`oint_(PQRS)vecB*vecdl = mu_0 `× Total current through rectangle PQRS
BL = μ0 × Number of turns in rectangle × Current
BL = μ0nLI
∴ B= μ0nI
APPEARS IN
संबंधित प्रश्न
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
Explain Ampere’s circuital law.
In Ampere's \[\oint \vec{B} \cdot d \vec{l} = \mu_0 i,\] the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
A thin but long, hollow, cylindrical tube of radius r carries i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
State Ampere’s circuital law.
Define ampere.
Ampere’s circuital law is given by _______.
Using Ampere’s circuital law, obtain an expression for magnetic flux density ‘B’ at a point near an infinitely long and straight conductor, carrying a current I.
