Advertisements
Advertisements
प्रश्न
Consider the situation described in the previous problem. Suppose the current i enters the loop at the points A and leaves it at the point B. Find the magnetic field at the centre of the loop.
उत्तर
The loop ABCD can be considered as a circuit with two resistances in parallel, one along branch AB and other along branch ADC.
As, the sides of the loop are identical, their resistances are also same.
Let the resistance of each side be r.
The resistance of branch AB = r
The resistance of branch ADC = 3r
The current in the branches are calculated as:
As current follow the least resistive path so
Current in branch AB = \[\frac{3i}{4}\]
Current in branch ADC = \[\frac{i}{4}\]
At the centre of the loop:
Magnetic field due to wire AD, DC and CB will be into the plane of paper according to right hand thumb rule.
Magnetic field due to wire AB will be out of the plane of paper according to right hand thumb rule.
Net magnetic field at the centre = BAD +BDC +BCB − BAB which will be out of the plane of paper.
As, perpendicular distance of the centre from every wire will be equal to \[\frac{a}{\sqrt{2}}\] and angle made by corner points of each side at the centre is \[45^\circ \] .
\[B_{AD} = \frac{\mu_0 (\frac{i}{4})}{4\pi(\frac{a}{\sqrt{2}})}(\sin45^\circ + \sin45^\circ )\]
\[ = \frac{\mu_0 i}{8\pi a}\]
\[ B_{AD} = B_{DC} = B_{CB} \]
\[ B_{AD} + B_{DC} + B_{CB} = B^, = \frac{3 \mu_0 i}{8\pi a}\]
\[ B_{AB} = \frac{\mu_0 (\frac{3i}{4})}{4\pi(\frac{a}{\sqrt{2}})}(\sin45^\circ + \sin45^\circ )\]
\[ = \frac{3 \mu_0 i}{8\pi a}\]
\[ B_{net} = B^, - B_{AB} \]
\[ = 0\]
APPEARS IN
संबंधित प्रश्न
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire?
Explain Ampere’s circuital law.
A long, straight wire carries a current. Is Ampere's law valid for a loop that does not enclose the wire, or that encloses the wire but is not circular?
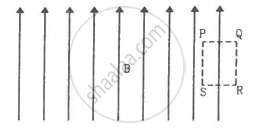
Sometimes we show an idealised magnetic field which is uniform in a given region and falls to zero abruptly. One such field is represented in figure. Using Ampere's law over the path PQRS, show that such a field is not possible.
Consider the situation of the previous problem. A particle having charge q and mass mis projected from the point Q in a direction going into the plane of the diagram. It is found to describe a circle of radius r between the two plates. Find the speed of the charged particle.
What is magnetic permeability?
Find the magnetic field due to a long straight conductor using Ampere’s circuital law.
Ampere’s circuital law is given by _______.
Two identical current carrying coaxial loops, carry current I in opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C, then which statement is correct?
A long solenoid having 200 turns per cm carries a current of 1.5 amp. At the centre of it is placed a coil of 100 turns of cross-sectional area 3.14 × 10−4 m2 having its axis parallel to the field produced by the solenoid. When the direction of current in the solenoid is reversed within 0.05 sec, the induced e.m.f. in the coil is:
Ampere's circuital law is used to find out ______
A long straight wire of radius 'a' carries a steady current 'I'. The current is uniformly distributed across its area of cross-section. The ratio of the magnitude of magnetic field `vecB_1` at `a/2` and `vecB_2` at distance 2a is ______.
The given figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r < a and r > a.