Advertisements
Advertisements
प्रश्न
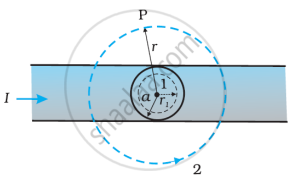
The given figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r < a and r > a.
उत्तर

- Consider the case r > a. The Amperian loop, labelled 2, is a circle concentric with a cross-section. For this loop, L = 2πr
Using Ampere circuital Law, we can write,
B(2πr) = μ0I, `B = (mu_0I)/(2pir), B ∝ 1/r` (r > a) - Consider the case r < a. The Amperian loop is a circle labelled 1. For this loop, taking the radius of the circle to be r, L = 2πr
Now the current enclosed Ie is not I but is less than this value. Since the current distribution is uniform, the current enclosed is,
`I_e = I((pir^2)/(pia^2)) = (Ir^2)/a^2` Using Ampere’s law, B(2πr) = `mu_0 (Ir^2)/a^2`
B = `((mu_0I)/(2pia^2))r`
B ∝ r (r < a)
APPEARS IN
संबंधित प्रश्न
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire?
In Ampere's \[\oint \vec{B} \cdot d \vec{l} = \mu_0 i,\] the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
Consider the situation described in the previous problem. Suppose the current i enters the loop at the points A and leaves it at the point B. Find the magnetic field at the centre of the loop.
A thin but long, hollow, cylindrical tube of radius r carries i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
Find the magnetic field due to a long straight conductor using Ampere’s circuital law.
In a capillary tube, the water rises by 1.2 mm. The height of water that will rise in another capillary tube having half the radius of the first is:
Two concentric and coplanar circular loops P and Q have their radii in the ratio 2:3. Loop Q carries a current 9 A in the anticlockwise direction. For the magnetic field to be zero at the common centre, loop P must carry ______.
A long straight wire of radius 'a' carries a steady current 'I'. The current is uniformly distributed across its area of cross-section. The ratio of the magnitude of magnetic field `vecB_1` at `a/2` and `vecB_2` at distance 2a is ______.
When current flowing through a solenoid decreases from 5A to 0 in 20 milliseconds, an emf of 500V is induced in it.
- What is this phenomenon called?
- Calculate coefficient of self-inductance of the solenoid.
