Advertisements
Advertisements
प्रश्न
The given figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r < a and r > a.
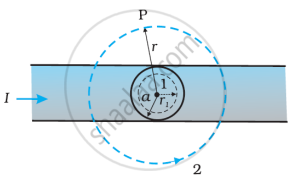
उत्तर

- Consider the case r > a. The Amperian loop, labelled 2, is a circle concentric with a cross-section. For this loop, L = 2πr
Using Ampere circuital Law, we can write,
B(2πr) = μ0I, `B = (mu_0I)/(2pir), B ∝ 1/r` (r > a) - Consider the case r < a. The Amperian loop is a circle labelled 1. For this loop, taking the radius of the circle to be r, L = 2πr
Now the current enclosed Ie is not I but is less than this value. Since the current distribution is uniform, the current enclosed is,
`I_e = I((pir^2)/(pia^2)) = (Ir^2)/a^2` Using Ampere’s law, B(2πr) = `mu_0 (Ir^2)/a^2`
B = `((mu_0I)/(2pia^2))r`
B ∝ r (r < a)
APPEARS IN
संबंधित प्रश्न
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
Using Ampere's circuital law, obtain an expression for the magnetic flux density 'B' at a point 'X' at a perpendicular distance 'r' from a long current-carrying conductor.
(Statement of the law is not required).
The wires which connect the battery of an automobile to its starting motor carry a current of 300 A (for a short time). What is the force per unit length between the wires if they are 70 cm long and 1.5 cm apart? Is the force attractive or repulsive?
Ampere’s circuital law is given by _______.
The force required to double the length of a steel wire of area 1 cm2, if it's Young's modulus Y = `2 xx 10^11/m^2` is:
Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C ______.
- `oint B.dl = +- 2μ_0I`
- the value of `oint B.dl` is independent of sense of C.
- there may be a point on C where B and dl are perpendicular.
- B vanishes everywhere on C.
Two concentric and coplanar circular loops P and Q have their radii in the ratio 2:3. Loop Q carries a current 9 A in the anticlockwise direction. For the magnetic field to be zero at the common centre, loop P must carry ______.
Using Ampere’s circuital law, obtain an expression for magnetic flux density ‘B’ at a point near an infinitely long and straight conductor, carrying a current I.
