Advertisements
Advertisements
प्रश्न
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
उत्तर
Maxwell's generalisation of Ampere's circuital law is given as follows:
`ointvecB.vec"dl"=mu_0(I+I_D)=mu_0(I+varepsilon_0 (dphi)/dt)`
Consider that a parallel capacitor C is charging in a circuit.
The magnitude of electric field between the two plates will be `E=q/(varepsilon_0 A)`and is perpendicular to the surface of the plate.
`phi_E=vecE.vecA=EA cos0=q/(varepsilon_0 A)xxA=q/varepsilon_0`
`=>(dphi_E)/dt=(d(q/varepsilon_0))/dt`
`=>(dq)/dt=varepsilon_0(dphi_E)/dt ("Here, dq/dt is rate of change of charge with time.")`
`=>I=varepsilon_0(dphi_E)/dt`
APPEARS IN
संबंधित प्रश्न
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
State Ampere’s circuital law.
Electron drift speed is estimated to be of the order of mm s−1. Yet large current of the order of few amperes can be set up in the wire. Explain briefly.
Consider the situation described in the previous problem. Suppose the current i enters the loop at the points A and leaves it at the point B. Find the magnetic field at the centre of the loop.
Sometimes we show an idealised magnetic field which is uniform in a given region and falls to zero abruptly. One such field is represented in figure. Using Ampere's law over the path PQRS, show that such a field is not possible.
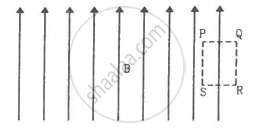
What is magnetic permeability?
Calculate the magnetic field inside and outside of the long solenoid using Ampere’s circuital law
Ampere’s circuital law is given by _______.
In a capillary tube, the water rises by 1.2 mm. The height of water that will rise in another capillary tube having half the radius of the first is:
