Advertisements
Advertisements
Question
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
Solution
Maxwell's generalisation of Ampere's circuital law is given as follows:
`ointvecB.vec"dl"=mu_0(I+I_D)=mu_0(I+varepsilon_0 (dphi)/dt)`
Consider that a parallel capacitor C is charging in a circuit.
The magnitude of electric field between the two plates will be `E=q/(varepsilon_0 A)`and is perpendicular to the surface of the plate.
`phi_E=vecE.vecA=EA cos0=q/(varepsilon_0 A)xxA=q/varepsilon_0`
`=>(dphi_E)/dt=(d(q/varepsilon_0))/dt`
`=>(dq)/dt=varepsilon_0(dphi_E)/dt ("Here, dq/dt is rate of change of charge with time.")`
`=>I=varepsilon_0(dphi_E)/dt`
APPEARS IN
RELATED QUESTIONS
A thin but long, hollow, cylindrical tube of radius r carries i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
A solid wire of radius 10 cm carries a current of 5.0 A distributed uniformly over its cross section. Find the magnetic field B at a point at a distance (a) 2 cm (b) 10 cm and (c) 20 cm away from the axis. Sketch a graph B versus x for 0 < x < 20 cm.
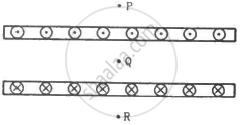
Two large metal sheets carry currents as shown in figure. The current through a strip of width dl is Kdl where K is a constant. Find the magnetic field at the points P, Q and R.
Using Ampere's circuital law, obtain an expression for the magnetic flux density 'B' at a point 'X' at a perpendicular distance 'r' from a long current-carrying conductor.
(Statement of the law is not required).
Find the magnetic field due to a long straight conductor using Ampere’s circuital law.
A solenoid of length 0.6 m has a radius of 2 cm and is made up of 600 turns If it carries a current of 4 A, then the magnitude of the magnetic field inside the solenoid is:
Two concentric and coplanar circular loops P and Q have their radii in the ratio 2:3. Loop Q carries a current 9 A in the anticlockwise direction. For the magnetic field to be zero at the common centre, loop P must carry ______.
Using Ampere’s circuital law, obtain an expression for magnetic flux density ‘B’ at a point near an infinitely long and straight conductor, carrying a current I.
