Advertisements
Advertisements
Question
Using Ampere's circuital law, obtain an expression for the magnetic flux density 'B' at a point 'X' at a perpendicular distance 'r' from a long current-carrying conductor.
(Statement of the law is not required).
Solution
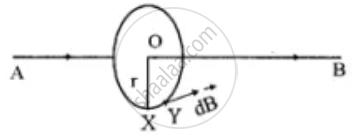
Let AB, a long straight wire is carrying current i. The magnetic flux density `bar(B)` is to be required at point X at a distance r.
Let us draw a circle of radius r with centre O as shown in above figure. The point X lies on the circumference of the circle.
According to Ampere's circuital law,
`oint bar(B). bar(dl)= μ_0i. "where " bar(dl)` = infinitesimally small portion XY in the circle.
For complete circle, `bar(dl)= 2pir`
∴ `bar(B). 2pir = μ_0i`
⇒ `bar (B) = (mu_0)/(2pi).i/r NA^(-1)m^(- 1)`
⇒ `bar (B) = (mu_0)/(4pi).(2i)/r`
∴ `bar (B) = 10^-7 .(2i)/r NA^(-1)m^(- 1)`
APPEARS IN
RELATED QUESTIONS
Electron drift speed is estimated to be of the order of mm s−1. Yet large current of the order of few amperes can be set up in the wire. Explain briefly.
Obtain an expression for magnetic induction along the axis of the toroid.
In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero
(a) outside the cable
(b) inside the inner conductor
(c) inside the outer conductor
(d) in between the tow conductors.
Consider the situation described in the previous problem. Suppose the current i enters the loop at the points A and leaves it at the point B. Find the magnetic field at the centre of the loop.
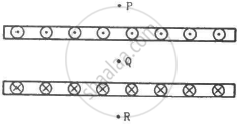
Two large metal sheets carry currents as shown in figure. The current through a strip of width dl is Kdl where K is a constant. Find the magnetic field at the points P, Q and R.
Ampere’s circuital law is given by _______.
Two identical current carrying coaxial loops, carry current I in opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C, then which statement is correct?
Read the following paragraph and answer the questions.
|
Consider the experimental set-up shown in the figure. This jumping ring experiment is an outstanding demonstration of some simple laws of Physics. A conducting non-magnetic ring is placed over the vertical core of a solenoid. When current is passed through the solenoid, the ring is thrown off. |
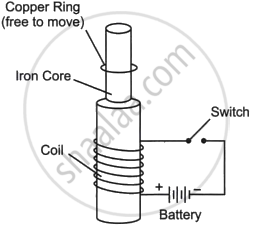
- Explain the reason for the jumping of the ring when the switch is closed in the circuit.
- What will happen if the terminals of the battery are reversed and the switch is closed? Explain.
- Explain the two laws that help us understand this phenomenon.
Using Ampere’s circuital law, obtain an expression for magnetic flux density ‘B’ at a point near an infinitely long and straight conductor, carrying a current I.
