Advertisements
Advertisements
Question
In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero
(a) outside the cable
(b) inside the inner conductor
(c) inside the outer conductor
(d) in between the tow conductors.
Solution
(a) outside the cable
(b) inside the inner conductor
According to Ampere's law, in a coaxial, straight cable carrying currents i in the inner conductor and -i (equally in the opposite direction) in the outside conductor.
Inside the inner conductor
\[\oint \vec{B} . d \vec{l} = \mu_o i_{\text{ inside }} \]
\[\oint \vec{B} . d \vec{l} = 0\]
\[ \Rightarrow B . l = 0\]
\[ \Rightarrow B = 0\]
In between the 2 conductors
\[\oint \vec{B} . d \vec{l} = \mu_o i\]
\[ \Rightarrow B = \frac{\mu_o i}{2\pi r}\]
Outside the outer conductor
\[\oint \vec{B} . d \vec{l} = \mu_o (i - i)\]
\[ \Rightarrow B = 0\]
Therefore, the magnetic field is zero outside the cable.
APPEARS IN
RELATED QUESTIONS
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
State Ampere’s circuital law.
Using Ampere’s circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis ?
In order to have a current in a long wire, it should be connected to a battery or some such device. Can we obtain the magnetic due to a straight, long wire by using Ampere's law without mentioning this other part of the circuit?
A long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnitude filed at a point (a) just inside the tube (b) just outside the tube.
State Ampere’s circuital law.
Define ampere.
Find the magnetic field due to a long straight conductor using Ampere’s circuital law.
Two identical current carrying coaxial loops, carry current I in opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C, then which statement is correct?
A solenoid of length 0.6 m has a radius of 2 cm and is made up of 600 turns If it carries a current of 4 A, then the magnitude of the magnetic field inside the solenoid is:
Ampere's circuital law is used to find out ______
Two concentric and coplanar circular loops P and Q have their radii in the ratio 2:3. Loop Q carries a current 9 A in the anticlockwise direction. For the magnetic field to be zero at the common centre, loop P must carry ______.
A long straight wire of radius 'a' carries a steady current 'I'. The current is uniformly distributed across its area of cross-section. The ratio of the magnitude of magnetic field `vecB_1` at `a/2` and `vecB_2` at distance 2a is ______.
Read the following paragraph and answer the questions.
|
Consider the experimental set-up shown in the figure. This jumping ring experiment is an outstanding demonstration of some simple laws of Physics. A conducting non-magnetic ring is placed over the vertical core of a solenoid. When current is passed through the solenoid, the ring is thrown off. |
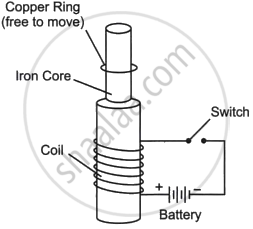
- Explain the reason for the jumping of the ring when the switch is closed in the circuit.
- What will happen if the terminals of the battery are reversed and the switch is closed? Explain.
- Explain the two laws that help us understand this phenomenon.
Briefly explain various ways to increase the strength of the magnetic field produced by a given solenoid.
