Advertisements
Advertisements
Question
State Ampere’s circuital law.
Solution 1
Statement: The line integral of the magnetic field `(vecB)` around any closed path is equal to μ0 times
the total current (I) passing through that closed path.
`:.ointvecB.vec(dl)=mu_0I`
Solution 2
Statement: The line integral of the magnetic field `(vecB)` around any closed path is equal to μ0 times
the total current (I) passing through that closed path.
`:.ointvecB.vec(dl)=mu_0I`
Solution 3
Ampere’s law states that the path integral or line integral over a closed loop of the magnetic field produced by a current distribution is given by `oint vec("B") . vec("dl") = µ_0"l"`
where I refers to the current enclosed by the loop.
Ampere’s law is a useful relation that is analogous to Gauss’s law of electrostatics. It is a relation between the tangential component of magnetic field at points on a closed curve and the net current through the area bounded by the curve.
To evaluate the expression for `oint vec("B") . vec("dl")` let us consider a long, straight conductor carrying a current I, passing through the centre of a circle of radius r in a plane perpendicular to the conductor.
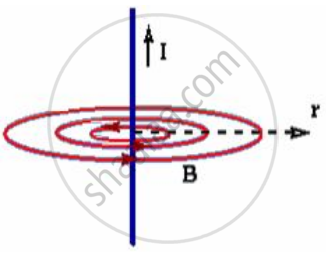
According to Biot-Savart law of magnetism, the field has a magnitude `(µ_0"l")/(2pir)` at every point on the circle, and it is tangent to the circle at each point.
The line integral of `vec("B")` around the circle is
`oint vec("B") . vec("dl") = oint(µ_0"I")/(2pir)"dl" = (µ_0"l")/(2pir) oint"dl"`
Since `ointvec("dI") = 2pir` is the circumference of the circle,
Therefore , `oint vec("B") . vec("dl") = µ_0"l"`
APPEARS IN
RELATED QUESTIONS
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire?
Obtain an expression for magnetic induction along the axis of the toroid.
In Ampere's \[\oint \vec{B} \cdot d \vec{l} = \mu_0 i,\] the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
In order to have a current in a long wire, it should be connected to a battery or some such device. Can we obtain the magnetic due to a straight, long wire by using Ampere's law without mentioning this other part of the circuit?
Consider the situation described in the previous problem. Suppose the current i enters the loop at the points A and leaves it at the point B. Find the magnetic field at the centre of the loop.
A long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnitude filed at a point (a) just inside the tube (b) just outside the tube.
A solid wire of radius 10 cm carries a current of 5.0 A distributed uniformly over its cross section. Find the magnetic field B at a point at a distance (a) 2 cm (b) 10 cm and (c) 20 cm away from the axis. Sketch a graph B versus x for 0 < x < 20 cm.
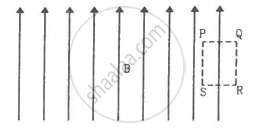
Sometimes we show an idealised magnetic field which is uniform in a given region and falls to zero abruptly. One such field is represented in figure. Using Ampere's law over the path PQRS, show that such a field is not possible.
Using Ampere's circuital law, obtain an expression for the magnetic flux density 'B' at a point 'X' at a perpendicular distance 'r' from a long current-carrying conductor.
(Statement of the law is not required).
What is magnetic permeability?
Define ampere.
Find the magnetic field due to a long straight conductor using Ampere’s circuital law.
A straight wire of diameter 0.5 mm carrying a current of 1 A is replaced by another wire of 1 mm diameter carrying the same current. The strength of the magnetic field far away is ______.
Two identical current carrying coaxial loops, carry current I in opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C, then which statement is correct?
In a capillary tube, the water rises by 1.2 mm. The height of water that will rise in another capillary tube having half the radius of the first is:
A thick current carrying cable of radius ‘R’ carries current ‘I’ uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance ‘r’ from the axis of the cable is represented by:
Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C ______.
- `oint B.dl = +- 2μ_0I`
- the value of `oint B.dl` is independent of sense of C.
- there may be a point on C where B and dl are perpendicular.
- B vanishes everywhere on C.
Two concentric and coplanar circular loops P and Q have their radii in the ratio 2:3. Loop Q carries a current 9 A in the anticlockwise direction. For the magnetic field to be zero at the common centre, loop P must carry ______.
A long straight wire of radius 'a' carries a steady current 'I'. The current is uniformly distributed across its area of cross-section. The ratio of the magnitude of magnetic field `vecB_1` at `a/2` and `vecB_2` at distance 2a is ______.
Read the following paragraph and answer the questions.
|
Consider the experimental set-up shown in the figure. This jumping ring experiment is an outstanding demonstration of some simple laws of Physics. A conducting non-magnetic ring is placed over the vertical core of a solenoid. When current is passed through the solenoid, the ring is thrown off. |
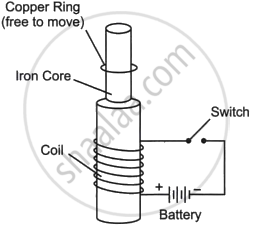
- Explain the reason for the jumping of the ring when the switch is closed in the circuit.
- What will happen if the terminals of the battery are reversed and the switch is closed? Explain.
- Explain the two laws that help us understand this phenomenon.
Briefly explain various ways to increase the strength of the magnetic field produced by a given solenoid.
Using Ampere’s circuital law, obtain an expression for magnetic flux density ‘B’ at a point near an infinitely long and straight conductor, carrying a current I.
