Advertisements
Advertisements
Question
Calculate the radius of second Bohr orbit in hydrogen atom from the given data.
Mass of electron = 9.1 x 10-31kg
Charge on the electron = 1.6 x 10-19 C
Planck’s constant = 6.63 x 10-34 J-s.
Permittivity of free space = 8.85 x 10-12 C2/Nm2
Solution
`r_n=((h^2epsilon_0)/(pime^2))n^2`
`:.r_2=((h^2epsilon_0)/(pime^2))(2)^2`
`r_2=((6.63xx10^(-34))^2xx8.85xx10^(-12)xx(2)^2)/(3.14xx9.1xx10^(-31)xx(1.6xx10^(-19))^2)`
`=(43.96 xx 10^-68 xx 8.85 xx 10^-12 xx 4)/(3.14 xx 9.1 xx 10^-31 xx 2.56 xx 10^-38)`
=2.127x10-10m
=2.127 A°
APPEARS IN
RELATED QUESTIONS
(i) State Bohr's quantization condition for defining stationary orbits. How does the de Broglie hypothesis explain the stationary orbits?
(ii) Find the relation between three wavelengths λ1, λ2 and λ3 from the energy-level diagram shown below.
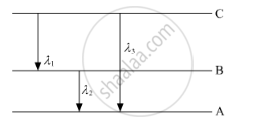
Draw a neat, labelled energy level diagram for H atom showing the transitions. Explain the series of spectral lines for H atom, whose fixed inner orbit numbers are 3 and 4 respectively.
The longest wavelength doublet absorption transition is observed at 589 and 589.6 nm. Calculate the frequency of each transition and energy difference between two excited states.
(a) Using the Bohr’s model calculate the speed of the electron in a hydrogen atom in the n = 1, 2, and 3 levels.
(b) Calculate the orbital period in each of these levels.
In accordance with the Bohr’s model, find the quantum number that characterises the earth’s revolution around the sun in an orbit of radius 1.5 × 1011 m with orbital speed 3 × 104 m/s. (Mass of earth = 6.0 × 1024 kg)
if `E_p` and `E_k` represent potential energy and kinetic energy respectively, of an orbital electron, then, according to B9hr's theory:
a)`E_k = -E_p"/"2`
b) `E_k = -E_p`
c) `E_k = -2E_p`
d) `E_k = 2E_p`
Using Bohr’s postulates, derive the expression for the frequency of radiation emitted when electron in hydrogen atom undergoes transition from higher energy state (quantum number ni) to the lower state, (nf).
When electron in hydrogen atom jumps from energy state ni = 4 to nf = 3, 2, 1, identify the spectral series to which the emission lines belong.
The Bohr radius is given by `a_0 = (∈_0h^2)/{pime^2}`. Verify that the RHS has dimensions of length.
A parallel beam of light of wavelength 100 nm passes through a sample of atomic hydrogen gas in ground state. (a) Assume that when a photon supplies some of its energy to a hydrogen atom, the rest of the energy appears as another photon. Neglecting the light emitted by the excited hydrogen atoms in the direction of the incident beam, what wavelengths may be observed in the transmitted beam? (b) A radiation detector is placed near the gas to detect radiation coming perpendicular to the incident beam. Find the wavelengths of radiation that may be detected by the detector.
When a photon is emitted by a hydrogen atom, the photon carries a momentum with it. (a) Calculate the momentum carries by the photon when a hydrogen atom emits light of wavelength 656.3 nm. (b) With what speed does the atom recoil during this transition? Take the mass of the hydrogen atom = 1.67 × 10−27 kg. (c) Find the kinetic energy of recoil of the atom.
Consider a neutron and an electron bound to each other due to gravitational force. Assuming Bohr's quantization rule for angular momentum to be valid in this case, derive an expression for the energy of the neutron-electron system.
Answer the following question.
Calculate the orbital period of the electron in the first excited state of the hydrogen atom.
Answer the following question.
Calculate the de-Broglie wavelength associated with the electron revolving in the first excited state of the hydrogen atom. The ground state energy of the hydrogen atom is – 13.6 eV.
Using Bohr's postulates derive the expression for the radius of nth orbit of the electron.
Ratio of longest to shortest wavelength in Balmer series is ______.
Hydrogen atom has only one electron, so mutual repulsion between electrons is absent. However, in multielectron atoms mutual repulsion between the electrons is significant. How does this affect the energy of an electron in the orbitals of the same principal quantum number in multielectron atoms?
Calculate the energy and frequency of the radiation emitted when an electron jumps from n = 3 to n = 2 in a hydrogen atom.
Derive an expression for the frequency of radiation emitted when a hydrogen atom de-excites from level n to level (n – 1). Also show that for large values of n, this frequency equals to classical frequency of revolution of an electron.
According to Bhor' s theory the moment of momentum of an electron revolving in second orbit of hydrogen atom will be.
The simple Bohr model cannot be directly applied to calculate the energy levels of an atom with many electrons. This is because ______.
According to Bohr atom model, in which of the following transitions will the frequency be maximum?
A 100 eV electron collides with a stationary helium ion (He+) in its ground state and exits to a higher level. After the collision, He+ ions emit two photons in succession with wavelengths 1085 Å and 304 Å. The energy of the electron after the collision will be ______ eV.
Given h = 6.63 × 10-34 Js.
What is the energy of an electron in stationary state corresponding to n = 2?
According to Bohr's theory, the radius of the nth Bohr orbit of a hydrogen like atom of atomic number Z is proportional to ______.
How much is the angular momentum of an electron when it is orbiting in the second Bohr orbit of hydrogen atom?
On the basis of Bohr's theory, derive an expression for the radius of the nth orbit of an electron of hydrogen atom.
State the Bohr's postulate of angular momentum of an electron.
