Advertisements
Advertisements
प्रश्न
Using Ampere's circuital law, obtain an expression for the magnetic flux density 'B' at a point 'X' at a perpendicular distance 'r' from a long current-carrying conductor.
(Statement of the law is not required).
उत्तर
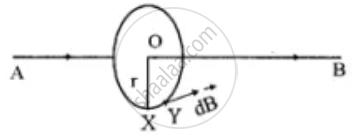
Let AB, a long straight wire is carrying current i. The magnetic flux density `bar(B)` is to be required at point X at a distance r.
Let us draw a circle of radius r with centre O as shown in above figure. The point X lies on the circumference of the circle.
According to Ampere's circuital law,
`oint bar(B). bar(dl)= μ_0i. "where " bar(dl)` = infinitesimally small portion XY in the circle.
For complete circle, `bar(dl)= 2pir`
∴ `bar(B). 2pir = μ_0i`
⇒ `bar (B) = (mu_0)/(2pi).i/r NA^(-1)m^(- 1)`
⇒ `bar (B) = (mu_0)/(4pi).(2i)/r`
∴ `bar (B) = 10^-7 .(2i)/r NA^(-1)m^(- 1)`
APPEARS IN
संबंधित प्रश्न
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
State Ampere’s circuital law.
Electron drift speed is estimated to be of the order of mm s−1. Yet large current of the order of few amperes can be set up in the wire. Explain briefly.
A hollow tube is carrying an electric current along its length distributed uniformly over its surface. The magnetic field
(a) increases linearly from the axis to the surface
(b) is constant inside the tube
(c) is zero at the axis
(d) is zero just outside the tube.
Consider the situation described in the previous problem. Suppose the current i enters the loop at the points A and leaves it at the point B. Find the magnetic field at the centre of the loop.
A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
What is magnetic permeability?
The force required to double the length of a steel wire of area 1 cm2, if it's Young's modulus Y = `2 xx 10^11/m^2` is:
Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C ______.
- `oint B.dl = +- 2μ_0I`
- the value of `oint B.dl` is independent of sense of C.
- there may be a point on C where B and dl are perpendicular.
- B vanishes everywhere on C.
The given figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r < a and r > a.