Advertisements
Advertisements
प्रश्न
A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
उत्तर
Given:
Magnitude of current = i
Radius of the wire = b
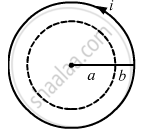
For a point at a distance a from the axis,
Current enclosed,
\[i' = \frac{i}{\pi b^2} \times \pi a^2\]
By Ampere's circuital law,
\[B \times 2\pi a = \mu_0 \frac{i}{\pi b^2} \times \pi a^2 \]
\[ \Rightarrow B = \frac{\mu_0 ia}{2\pi b^2}\]
APPEARS IN
संबंधित प्रश्न
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
State Ampere’s circuital law.
Electron drift speed is estimated to be of the order of mm s−1. Yet large current of the order of few amperes can be set up in the wire. Explain briefly.
Using Ampere’s circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis ?
A long, straight wire carries a current. Is Ampere's law valid for a loop that does not enclose the wire, or that encloses the wire but is not circular?
A thin but long, hollow, cylindrical tube of radius r carries i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
A long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnitude filed at a point (a) just inside the tube (b) just outside the tube.
Sometimes we show an idealised magnetic field which is uniform in a given region and falls to zero abruptly. One such field is represented in figure. Using Ampere's law over the path PQRS, show that such a field is not possible.
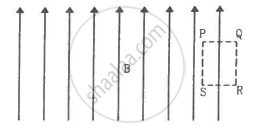
Consider the situation of the previous problem. A particle having charge q and mass mis projected from the point Q in a direction going into the plane of the diagram. It is found to describe a circle of radius r between the two plates. Find the speed of the charged particle.
Using Ampere's circuital law, obtain an expression for the magnetic flux density 'B' at a point 'X' at a perpendicular distance 'r' from a long current-carrying conductor.
(Statement of the law is not required).
State Ampere’s circuital law.
Define ampere.
Calculate the magnetic field inside and outside of the long solenoid using Ampere’s circuital law
The wires which connect the battery of an automobile to its starting motor carry a current of 300 A (for a short time). What is the force per unit length between the wires if they are 70 cm long and 1.5 cm apart? Is the force attractive or repulsive?
A solenoid of length 0.6 m has a radius of 2 cm and is made up of 600 turns If it carries a current of 4 A, then the magnitude of the magnetic field inside the solenoid is:
A long solenoid having 200 turns per cm carries a current of 1.5 amp. At the centre of it is placed a coil of 100 turns of cross-sectional area 3.14 × 10−4 m2 having its axis parallel to the field produced by the solenoid. When the direction of current in the solenoid is reversed within 0.05 sec, the induced e.m.f. in the coil is:
Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C ______.
- `oint B.dl = +- 2μ_0I`
- the value of `oint B.dl` is independent of sense of C.
- there may be a point on C where B and dl are perpendicular.
- B vanishes everywhere on C.
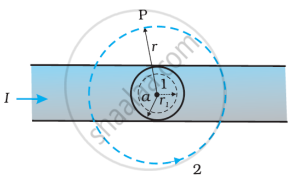
The given figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r < a and r > a.
When current flowing through a solenoid decreases from 5A to 0 in 20 milliseconds, an emf of 500V is induced in it.
- What is this phenomenon called?
- Calculate coefficient of self-inductance of the solenoid.
