Advertisements
Advertisements
Question
A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
Solution
Given:
Magnitude of current = i
Radius of the wire = b
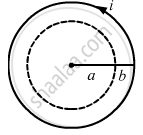
For a point at a distance a from the axis,
Current enclosed,
\[i' = \frac{i}{\pi b^2} \times \pi a^2\]
By Ampere's circuital law,
\[B \times 2\pi a = \mu_0 \frac{i}{\pi b^2} \times \pi a^2 \]
\[ \Rightarrow B = \frac{\mu_0 ia}{2\pi b^2}\]
APPEARS IN
RELATED QUESTIONS
State Ampere’s circuital law.
Using Ampere’s circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis ?
A long straight wire of a circular cross-section of radius ‘a’ carries a steady current ‘I’. The current is uniformly distributed across the cross-section. Apply Ampere’s circuital law to calculate the magnetic field at a point ‘r’ in the region for (i) r < a and (ii) r > a.
In order to have a current in a long wire, it should be connected to a battery or some such device. Can we obtain the magnetic due to a straight, long wire by using Ampere's law without mentioning this other part of the circuit?
A hollow tube is carrying an electric current along its length distributed uniformly over its surface. The magnetic field
(a) increases linearly from the axis to the surface
(b) is constant inside the tube
(c) is zero at the axis
(d) is zero just outside the tube.
Consider the situation described in the previous problem. Suppose the current i enters the loop at the points A and leaves it at the point B. Find the magnetic field at the centre of the loop.
A long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnitude filed at a point (a) just inside the tube (b) just outside the tube.
Consider the situation of the previous problem. A particle having charge q and mass mis projected from the point Q in a direction going into the plane of the diagram. It is found to describe a circle of radius r between the two plates. Find the speed of the charged particle.
Using Ampere's circuital law, obtain an expression for the magnetic flux density 'B' at a point 'X' at a perpendicular distance 'r' from a long current-carrying conductor.
(Statement of the law is not required).
Find the magnetic field due to a long straight conductor using Ampere’s circuital law.
Two identical current carrying coaxial loops, carry current I in opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C, then which statement is correct?
The force required to double the length of a steel wire of area 1 cm2, if it's Young's modulus Y = `2 xx 10^11/m^2` is:
Ampere's circuital law is used to find out ______
Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C ______.
- `oint B.dl = +- 2μ_0I`
- the value of `oint B.dl` is independent of sense of C.
- there may be a point on C where B and dl are perpendicular.
- B vanishes everywhere on C.
Read the following paragraph and answer the questions.
|
Consider the experimental set-up shown in the figure. This jumping ring experiment is an outstanding demonstration of some simple laws of Physics. A conducting non-magnetic ring is placed over the vertical core of a solenoid. When current is passed through the solenoid, the ring is thrown off. |
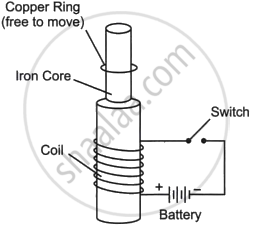
- Explain the reason for the jumping of the ring when the switch is closed in the circuit.
- What will happen if the terminals of the battery are reversed and the switch is closed? Explain.
- Explain the two laws that help us understand this phenomenon.
The given figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r < a and r > a.
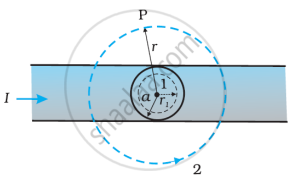
Using Ampere’s circuital law, obtain an expression for magnetic flux density ‘B’ at a point near an infinitely long and straight conductor, carrying a current I.
