Advertisements
Advertisements
Question
A long straight wire of a circular cross-section of radius ‘a’ carries a steady current ‘I’. The current is uniformly distributed across the cross-section. Apply Ampere’s circuital law to calculate the magnetic field at a point ‘r’ in the region for (i) r < a and (ii) r > a.
Solution
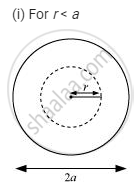
`ointvecB*vecdl = mu_0I_(enclosed)`
`(I_(enclosed))/(pia^2) = I/(pir^2)`
`I_(enclosed) = I r_2/a^2`
`vecB*vecdl = Bdl (because costheta = 1)`
`therefore ointBdl = mu_0Ir_2/a^2`
`Bointdl = mu_0Ir^2/a^2`
`B(2pir) = mu_0 Ir^2/a^2`
`B = (mu_0)/(2pi) I/a^2 r `
(ii) For r > a
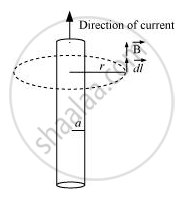
From Ampere’s circuital law,
`ointvecB*vecdl = mu_0 l_(enclosed)`
`vecB*vecdl =Bdt cos theta`
`theta = 0`
`I_(enclosed) = I`
`oint Bdl = mu_0I`
`Bointdl = mu_0I`
`B(2pir) = mu_0I`
`B= (mu_0)/(2pi) I/r`
APPEARS IN
RELATED QUESTIONS
A hollow tube is carrying an electric current along its length distributed uniformly over its surface. The magnetic field
(a) increases linearly from the axis to the surface
(b) is constant inside the tube
(c) is zero at the axis
(d) is zero just outside the tube.
A solid wire of radius 10 cm carries a current of 5.0 A distributed uniformly over its cross section. Find the magnetic field B at a point at a distance (a) 2 cm (b) 10 cm and (c) 20 cm away from the axis. Sketch a graph B versus x for 0 < x < 20 cm.
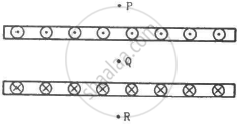
Two large metal sheets carry currents as shown in figure. The current through a strip of width dl is Kdl where K is a constant. Find the magnetic field at the points P, Q and R.
Define ampere.
Calculate the magnetic field inside and outside of the long solenoid using Ampere’s circuital law
Two identical current carrying coaxial loops, carry current I in opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C, then which statement is correct?
A solenoid of length 0.6 m has a radius of 2 cm and is made up of 600 turns If it carries a current of 4 A, then the magnitude of the magnetic field inside the solenoid is:
Two concentric and coplanar circular loops P and Q have their radii in the ratio 2:3. Loop Q carries a current 9 A in the anticlockwise direction. For the magnetic field to be zero at the common centre, loop P must carry ______.
Using Ampere’s circuital law, obtain an expression for magnetic flux density ‘B’ at a point near an infinitely long and straight conductor, carrying a current I.
