Advertisements
Advertisements
प्रश्न
A long straight wire of a circular cross-section of radius ‘a’ carries a steady current ‘I’. The current is uniformly distributed across the cross-section. Apply Ampere’s circuital law to calculate the magnetic field at a point ‘r’ in the region for (i) r < a and (ii) r > a.
उत्तर
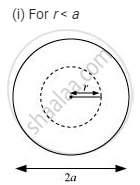
`ointvecB*vecdl = mu_0I_(enclosed)`
`(I_(enclosed))/(pia^2) = I/(pir^2)`
`I_(enclosed) = I r_2/a^2`
`vecB*vecdl = Bdl (because costheta = 1)`
`therefore ointBdl = mu_0Ir_2/a^2`
`Bointdl = mu_0Ir^2/a^2`
`B(2pir) = mu_0 Ir^2/a^2`
`B = (mu_0)/(2pi) I/a^2 r `
(ii) For r > a
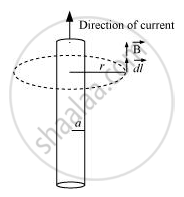
From Ampere’s circuital law,
`ointvecB*vecdl = mu_0 l_(enclosed)`
`vecB*vecdl =Bdt cos theta`
`theta = 0`
`I_(enclosed) = I`
`oint Bdl = mu_0I`
`Bointdl = mu_0I`
`B(2pir) = mu_0I`
`B= (mu_0)/(2pi) I/r`
APPEARS IN
संबंधित प्रश्न
State Ampere’s circuital law.
A thin but long, hollow, cylindrical tube of radius r carries i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
A long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnitude filed at a point (a) just inside the tube (b) just outside the tube.
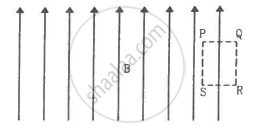
Sometimes we show an idealised magnetic field which is uniform in a given region and falls to zero abruptly. One such field is represented in figure. Using Ampere's law over the path PQRS, show that such a field is not possible.
Two large metal sheets carry currents as shown in figure. The current through a strip of width dl is Kdl where K is a constant. Find the magnetic field at the points P, Q and R.
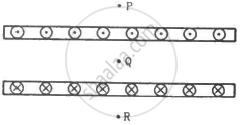
Consider the situation of the previous problem. A particle having charge q and mass mis projected from the point Q in a direction going into the plane of the diagram. It is found to describe a circle of radius r between the two plates. Find the speed of the charged particle.
What is magnetic permeability?
Two identical current carrying coaxial loops, carry current I in opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C, then which statement is correct?
A thick current carrying cable of radius ‘R’ carries current ‘I’ uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance ‘r’ from the axis of the cable is represented by ______
Two concentric and coplanar circular loops P and Q have their radii in the ratio 2:3. Loop Q carries a current 9 A in the anticlockwise direction. For the magnetic field to be zero at the common centre, loop P must carry ______.
