Advertisements
Advertisements
प्रश्न
A thin but long, hollow, cylindrical tube of radius r carries i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
Advertisements
उत्तर
(a) The magnetic field inside any conducting tube is always zero.
∴ Magnetic field inside the tube at a distance r/2 from the surface = 0
(b) Let the point outside the tube with distance \[\frac{r}{2}\] be P.
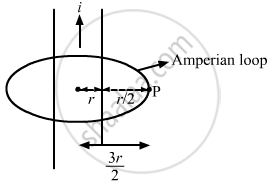
∴ Net distance from centre, r' = \[r + \frac{r}{2} = \frac{3r}{2}\]
Length of the loop, l = \[2\pi \times \frac{3}{2}r = 3\pi r\]
On applying Ampere's law, we get
\[ \Rightarrow B \times 3\pi r = \mu_0 i\]
\[ \Rightarrow B = \frac{\mu_0 i}{3\pi r}\]
APPEARS IN
संबंधित प्रश्न
Electron drift speed is estimated to be of the order of mm s−1. Yet large current of the order of few amperes can be set up in the wire. Explain briefly.
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire?
Obtain an expression for magnetic induction along the axis of the toroid.
A long straight wire of a circular cross-section of radius ‘a’ carries a steady current ‘I’. The current is uniformly distributed across the cross-section. Apply Ampere’s circuital law to calculate the magnetic field at a point ‘r’ in the region for (i) r < a and (ii) r > a.
In Ampere's \[\oint \vec{B} \cdot d \vec{l} = \mu_0 i,\] the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
A long, straight wire carries a current. Is Ampere's law valid for a loop that does not enclose the wire, or that encloses the wire but is not circular?
In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero
(a) outside the cable
(b) inside the inner conductor
(c) inside the outer conductor
(d) in between the tow conductors.
Two large metal sheets carry currents as shown in figure. The current through a strip of width dl is Kdl where K is a constant. Find the magnetic field at the points P, Q and R.
State Ampere’s circuital law.
Calculate the magnetic field inside and outside of the long solenoid using Ampere’s circuital law
Ampere’s circuital law is given by _______.
A thick current carrying cable of radius ‘R’ carries current ‘I’ uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance ‘r’ from the axis of the cable is represented by:
Two identical current carrying coaxial loops, carry current I in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C ______.
- `oint B.dl = +- 2μ_0I`
- the value of `oint B.dl` is independent of sense of C.
- there may be a point on C where B and dl are perpendicular.
- B vanishes everywhere on C.
Briefly explain various ways to increase the strength of the magnetic field produced by a given solenoid.
Using Ampere’s circuital law, obtain an expression for magnetic flux density ‘B’ at a point near an infinitely long and straight conductor, carrying a current I.
