Advertisements
Advertisements
प्रश्न
Calculate the magnetic field inside and outside of the long solenoid using Ampere’s circuital law
उत्तर
- Consider a solenoid of length L having N turns.
- Solenoid’s diameter is much smaller compared to its length.
The magnetic field inside the solenoid: - Consider a rectangular loop abcd.
- From Ampere’s circuital law,
- Elemental length bc and da are perpendicular to the magnetic field.
`therefore int_"b"^"c" vec"B" * vec"dl" = int_"b"^"c" |vec"B"| vec"dl" cos 90^circ = 0`
`int_"d"^"a" vec"B" * vec"d1" = 0`
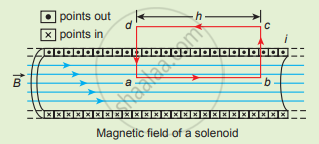
Amperian loop for solenoid
`oint_"C" vec"B" * vec"d1" = mu_0"I"_"enclosed"`
`oint_"C" vec"B"*vec"d1" = int_"a"^"b" vec"B" * vec"d1" + int_"b"^"c" vec"B"*vec"d1" + int_"c"^"d" vec"B" * vec"d1" + int_"d"^"a" vec"B" * vec"d1"`
Magnetic field outside the solenoid is zero
`int_"c"^"d" vec"B"*vec"dl" = 0`
For the path ab, `int_"a"^"b" vec"B"*vec"dl" = "B" int_"a"^"b" "dl" cos theta`
`= "B" int_"a"^"b" "dl"`
`= int_"a"^"b" vec"B" * vec"dl"` = BL
L - length of the solenoids
I - current passiing through the solenoid
N - Number of turns per unit length
`int_"a"^"b" vec"B"*vec"dl" = "BL" = mu_0"NI"`
B = `(mu_0 "NI")/"L"`
`"N"/"L" = "n"`
∴ `"N"/"L" = "n"`
∴ B = `mu_0 "nI"`
APPEARS IN
संबंधित प्रश्न
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
Obtain an expression for magnetic induction along the axis of the toroid.
Using Ampere’s circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis ?
A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
State Ampere’s circuital law.
Define ampere.
Two identical current carrying coaxial loops, carry current I in opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C, then which statement is correct?
A long straight wire of radius 'a' carries a steady current 'I'. The current is uniformly distributed across its area of cross-section. The ratio of the magnitude of magnetic field `vecB_1` at `a/2` and `vecB_2` at distance 2a is ______.
When current flowing through a solenoid decreases from 5A to 0 in 20 milliseconds, an emf of 500V is induced in it.
- What is this phenomenon called?
- Calculate coefficient of self-inductance of the solenoid.
