Advertisements
Advertisements
प्रश्न
Calculate the magnetic field inside and outside of the long solenoid using Ampere’s circuital law
उत्तर
- Consider a solenoid of length L having N turns.
- Solenoid’s diameter is much smaller compared to its length.
The magnetic field inside the solenoid: - Consider a rectangular loop abcd.
- From Ampere’s circuital law,
- Elemental length bc and da are perpendicular to the magnetic field.
`therefore int_"b"^"c" vec"B" * vec"dl" = int_"b"^"c" |vec"B"| vec"dl" cos 90^circ = 0`
`int_"d"^"a" vec"B" * vec"d1" = 0`
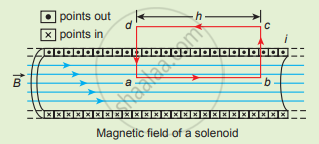
Amperian loop for solenoid
`oint_"C" vec"B" * vec"d1" = mu_0"I"_"enclosed"`
`oint_"C" vec"B"*vec"d1" = int_"a"^"b" vec"B" * vec"d1" + int_"b"^"c" vec"B"*vec"d1" + int_"c"^"d" vec"B" * vec"d1" + int_"d"^"a" vec"B" * vec"d1"`
Magnetic field outside the solenoid is zero
`int_"c"^"d" vec"B"*vec"dl" = 0`
For the path ab, `int_"a"^"b" vec"B"*vec"dl" = "B" int_"a"^"b" "dl" cos theta`
`= "B" int_"a"^"b" "dl"`
`= int_"a"^"b" vec"B" * vec"dl"` = BL
L - length of the solenoids
I - current passiing through the solenoid
N - Number of turns per unit length
`int_"a"^"b" vec"B"*vec"dl" = "BL" = mu_0"NI"`
B = `(mu_0 "NI")/"L"`
`"N"/"L" = "n"`
∴ `"N"/"L" = "n"`
∴ B = `mu_0 "nI"`
APPEARS IN
संबंधित प्रश्न
Explain Ampere’s circuital law.
Using Ampere’s circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis ?
A long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnitude filed at a point (a) just inside the tube (b) just outside the tube.
A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
Consider the situation of the previous problem. A particle having charge q and mass mis projected from the point Q in a direction going into the plane of the diagram. It is found to describe a circle of radius r between the two plates. Find the speed of the charged particle.
What is magnetic permeability?
Two identical current carrying coaxial loops, carry current I in opposite sense. A simple amperian loop passes through both of them once. Calling the loop as C, then which statement is correct?
A thick current carrying cable of radius ‘R’ carries current ‘I’ uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance ‘r’ from the axis of the cable is represented by ______
Using Ampere’s circuital law, obtain an expression for magnetic flux density ‘B’ at a point near an infinitely long and straight conductor, carrying a current I.
When current flowing through a solenoid decreases from 5A to 0 in 20 milliseconds, an emf of 500V is induced in it.
- What is this phenomenon called?
- Calculate coefficient of self-inductance of the solenoid.
