Advertisements
Advertisements
Question
Calculate the magnetic field inside and outside of the long solenoid using Ampere’s circuital law
Solution
- Consider a solenoid of length L having N turns.
- Solenoid’s diameter is much smaller compared to its length.
The magnetic field inside the solenoid: - Consider a rectangular loop abcd.
- From Ampere’s circuital law,
- Elemental length bc and da are perpendicular to the magnetic field.
`therefore int_"b"^"c" vec"B" * vec"dl" = int_"b"^"c" |vec"B"| vec"dl" cos 90^circ = 0`
`int_"d"^"a" vec"B" * vec"d1" = 0`
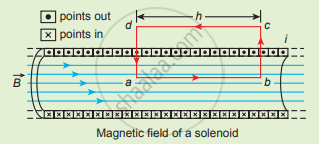
Amperian loop for solenoid
`oint_"C" vec"B" * vec"d1" = mu_0"I"_"enclosed"`
`oint_"C" vec"B"*vec"d1" = int_"a"^"b" vec"B" * vec"d1" + int_"b"^"c" vec"B"*vec"d1" + int_"c"^"d" vec"B" * vec"d1" + int_"d"^"a" vec"B" * vec"d1"`
Magnetic field outside the solenoid is zero
`int_"c"^"d" vec"B"*vec"dl" = 0`
For the path ab, `int_"a"^"b" vec"B"*vec"dl" = "B" int_"a"^"b" "dl" cos theta`
`= "B" int_"a"^"b" "dl"`
`= int_"a"^"b" vec"B" * vec"dl"` = BL
L - length of the solenoids
I - current passiing through the solenoid
N - Number of turns per unit length
`int_"a"^"b" vec"B"*vec"dl" = "BL" = mu_0"NI"`
B = `(mu_0 "NI")/"L"`
`"N"/"L" = "n"`
∴ `"N"/"L" = "n"`
∴ B = `mu_0 "nI"`
APPEARS IN
RELATED QUESTIONS
Explain Ampere’s circuital law.
In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero
(a) outside the cable
(b) inside the inner conductor
(c) inside the outer conductor
(d) in between the tow conductors.
Using Ampere's circuital law, obtain an expression for the magnetic flux density 'B' at a point 'X' at a perpendicular distance 'r' from a long current-carrying conductor.
(Statement of the law is not required).
Define ampere.
In a capillary tube, the water rises by 1.2 mm. The height of water that will rise in another capillary tube having half the radius of the first is:
A long solenoid having 200 turns per cm carries a current of 1.5 amp. At the centre of it is placed a coil of 100 turns of cross-sectional area 3.14 × 10−4 m2 having its axis parallel to the field produced by the solenoid. When the direction of current in the solenoid is reversed within 0.05 sec, the induced e.m.f. in the coil is:
A thick current carrying cable of radius ‘R’ carries current ‘I’ uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance ‘r’ from the axis of the cable is represented by:
A thick current carrying cable of radius ‘R’ carries current ‘I’ uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance ‘r’ from the axis of the cable is represented by ______
