Advertisements
Advertisements
Question
A thin but long, hollow, cylindrical tube of radius r carries i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
Solution
(a) The magnetic field inside any conducting tube is always zero.
∴ Magnetic field inside the tube at a distance r/2 from the surface = 0
(b) Let the point outside the tube with distance \[\frac{r}{2}\] be P.
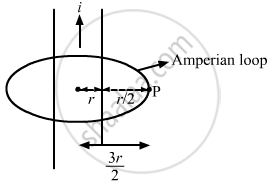
∴ Net distance from centre, r' = \[r + \frac{r}{2} = \frac{3r}{2}\]
Length of the loop, l = \[2\pi \times \frac{3}{2}r = 3\pi r\]
On applying Ampere's law, we get
\[ \Rightarrow B \times 3\pi r = \mu_0 i\]
\[ \Rightarrow B = \frac{\mu_0 i}{3\pi r}\]
APPEARS IN
RELATED QUESTIONS
Write Maxwell's generalization of Ampere's circuital law. Show that in the process of charging a capacitor, the current produced within the plates of the capacitor is `I=varepsilon_0 (dphi_E)/dt,`where ΦE is the electric flux produced during charging of the capacitor plates.
State Ampere’s circuital law.
State Ampere’s circuital law.
Obtain an expression for magnetic induction along the axis of the toroid.
Explain Ampere’s circuital law.
Using Ampere’s circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis ?
A long straight wire of a circular cross-section of radius ‘a’ carries a steady current ‘I’. The current is uniformly distributed across the cross-section. Apply Ampere’s circuital law to calculate the magnetic field at a point ‘r’ in the region for (i) r < a and (ii) r > a.
In Ampere's \[\oint \vec{B} \cdot d \vec{l} = \mu_0 i,\] the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero
(a) outside the cable
(b) inside the inner conductor
(c) inside the outer conductor
(d) in between the tow conductors.
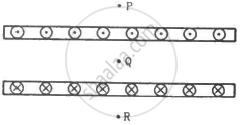
Two large metal sheets carry currents as shown in figure. The current through a strip of width dl is Kdl where K is a constant. Find the magnetic field at the points P, Q and R.
Using Ampere's circuital law, obtain an expression for the magnetic flux density 'B' at a point 'X' at a perpendicular distance 'r' from a long current-carrying conductor.
(Statement of the law is not required).
Define ampere.
Find the magnetic field due to a long straight conductor using Ampere’s circuital law.
Calculate the magnetic field inside and outside of the long solenoid using Ampere’s circuital law
Ampere’s circuital law is given by _______.
A thick current carrying cable of radius ‘R’ carries current ‘I’ uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance ‘r’ from the axis of the cable is represented by ______
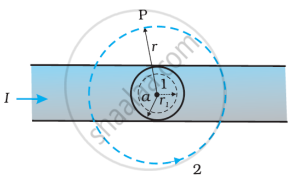
The given figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r < a and r > a.
Briefly explain various ways to increase the strength of the magnetic field produced by a given solenoid.
