Advertisements
Advertisements
Question
The given figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r < a and r > a.
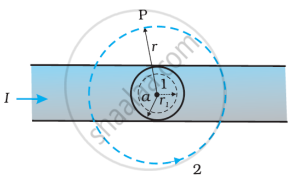
Solution

- Consider the case r > a. The Amperian loop, labelled 2, is a circle concentric with a cross-section. For this loop, L = 2πr
Using Ampere circuital Law, we can write,
B(2πr) = μ0I, `B = (mu_0I)/(2pir), B ∝ 1/r` (r > a) - Consider the case r < a. The Amperian loop is a circle labelled 1. For this loop, taking the radius of the circle to be r, L = 2πr
Now the current enclosed Ie is not I but is less than this value. Since the current distribution is uniform, the current enclosed is,
`I_e = I((pir^2)/(pia^2)) = (Ir^2)/a^2` Using Ampere’s law, B(2πr) = `mu_0 (Ir^2)/a^2`
B = `((mu_0I)/(2pia^2))r`
B ∝ r (r < a)
APPEARS IN
RELATED QUESTIONS
Electron drift speed is estimated to be of the order of mm s−1. Yet large current of the order of few amperes can be set up in the wire. Explain briefly.
A thin but long, hollow, cylindrical tube of radius r carries i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
A long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnitude filed at a point (a) just inside the tube (b) just outside the tube.
A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
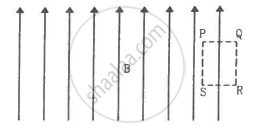
Sometimes we show an idealised magnetic field which is uniform in a given region and falls to zero abruptly. One such field is represented in figure. Using Ampere's law over the path PQRS, show that such a field is not possible.
Ampere’s circuital law is given by _______.
A thick current carrying cable of radius ‘R’ carries current ‘I’ uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance ‘r’ from the axis of the cable is represented by:
Briefly explain various ways to increase the strength of the magnetic field produced by a given solenoid.
