Advertisements
Advertisements
प्रश्न
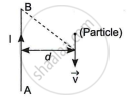
A long straight wire AB carries a current I. A particle (mass m and charge q) moves with a velocity `vec"v"`, parallel to the wire, at a distance d from it as shown in the figure. Obtain the expression for the force experienced by the particle and mention its directions.
उत्तर
Magnetic field induction at P due to current I in long straight wire AB is
`B = mu_0/(4pi) (2I)/d`
It acts perpendicular to the plane of the paper inward, represented by `hatn`.
Lorentz force acting on the particle at P can be given by
`vecF = q(vecv xx vecB) = e(vecv xx (mu_0. 2I)/(4pid)hatn)`
or `vecF = (mu_0Iev)/(2pid)(hatv xx hatn)`
∴ `F = (mu_0Iev)/(2pid)`
Acting in the plane of paper away from the wire.
संबंधित प्रश्न
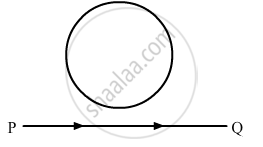
A conducting loop is held above a current carrying wire PQ as shown in the figure. Depict the direction of the current induced in the loop when the current in the wire PQ is constantly increasing.
Two wires carrying equal currents i each, are placed perpendicular to each other, just avoiding a contact. If one wire is held fixed and the other is free to move under magnetic forces, what kind of motion will result?
A charged particle is moved along a magnetic field line. The magnetic force on the particle is
State whether the following statement is true or false:
Magnetic poles exist in pairs.
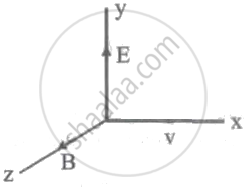
A particle with charge q moves with a velocity v in a direction perpendicular to the directions of uniform electric and magnetic fields, E and B respectively, which are mutually perpendicular to each other. Which one of the following gives the condition for which the particle moves undeflected in its original trajectory?
For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
B = `(μ_0"IR"^2"N")/(2("x"^2 + "R"^2)^(3/2))`
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by, B = `0.72 (μ_0"NI")/"R"` approximately.
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
Which one of the following is a correct statement about magnetic forces?
In the product `vec"F" = "q" (vec"υ" xx vec"B")`
= `"q" vec"υ" xx ("B"hat"i" +"B"hat"j" + "B"_0hat"k")`
For q = 1 and `vec"υ" = 2hat"i" + 4hat"j" + 6hat"k"` and
`vec"F" = 4hat"i" - 20hat"j" + 12hat"k"`
What will be the complete expression for `vec"B"`?
A cubical region of space is filled with some uniform electric and magnetic fields. An electron enters the cube across one of its faces with velocity v and a positron enters via opposite face with velocity – v. At this instant ______.
- the electric forces on both the particles cause identical accelerations.
- the magnetic forces on both the particles cause equal accelerations.
- both particles gain or loose energy at the same rate.
- the motion of the centre of mass (CM) is determined by B alone.
An electron is moving along positive x-axis in a magnetic field which is parallel to the positive y-axis. In what direction will the magnetic force be acting on the electron?
