Advertisements
Advertisements
प्रश्न
Two wires carrying equal currents i each, are placed perpendicular to each other, just avoiding a contact. If one wire is held fixed and the other is free to move under magnetic forces, what kind of motion will result?
उत्तर
The magnetic force on a wire carrying an electric current i is \[\vec{F} = i . ( \vec{l} \times \vec{B} )\] , where l is the length of the wire and B is the magnetic field acting on it. Suppose we have one wire in the horizontal direction (fixed) and other wire in the vertical direction (free to move). If the horizontal wire is carrying current from right to left is held fixed perpendicular to the vertical wire, which is free to move, the upper portion of the free wire will tend to move in the left direction and the lower portion of the wire will tend to move in the right direction, according to Fleming's left hand rule, as the magnetic field acting on the wire due to the fixed wire will point into the plane of paper above the wire and come out of the paper below the horizontal wire and the current will flow in upward direction in the free wire. Thus, the free wire will tend to become parallel to the fixed wire so as to experience maximum attractive force.
APPEARS IN
संबंधित प्रश्न
Two long, straight, parallel conductors carry steady currents, I1 and I2, separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other? Obtain the expression for this force. Hence, define one ampere.
A long straight wire carries a current of 35 A. What is the magnitude of the field B at a point 20 cm from the wire?
A charge ‘q’ moving along the X- axis with a velocity `vecv` is subjected to a uniform magnetic field B along the Z-axis as it crosses the origin O.
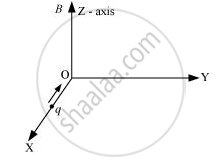
(i) Trace its trajectory.
(ii) Does the charge gain kinetic energy as it enters the magnetic field? Justify your answer.
A charged particle is in motion having initial velocity `vecv` when it enters into a region of uniform magnetic field perpendicular to `vecv`. Because of the magnetic force the kinetic energy of the particle will ______.
Explain "Magnetic force never does any work on moving charges".
For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
B = `(μ_0"IR"^2"N")/(2("x"^2 + "R"^2)^(3/2))`
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by, B = `0.72 (μ_0"NI")/"R"` approximately.
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
What is the magnetic induction of the field at the point O in a current I carrying wire that has the shape shown in the figure? The radius of the curved part of the wire is R, the linear parts are assumed to be very long.

Two charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field B = B0k̂.
An electron enters with a velocity v = v0i into a cubical region (faces parallel to coordinate planes) in which there are uniform electric and magnetic fields. The orbit of the electron is found to spiral down inside the cube in plane parallel to the x-y plane. Suggest a configuration of fields E and B that can lead to it.
At a certain place the angle of dip is 30° and the horizontal component of earth’s magnetic field is 0.5 G. The earth’s total magnetic field (in G), at that certain place, is ______.
Two conducting rails are connected to a source of emf and form an incline as shown in figure. A bar of mass 50 g slides without friction down the incline through a vertical magnetic field B. If the length of the bar is 50 cm and a current of 2.5 A is provided by battery. Value of B for which the bar slide at a constant velocity ______ × 10-1 Tesla. 2 [g = 10 m/s2]

Write the expression for the Lorentz force on a particle of charge q moving with a velocity `vecv` in a magnetic field `vecB`. When is the magnitude of this force maximum? Show that no work is done by this force on the particle during its motion from point `vecr_1` to point `vecr_2`.
A long straight conductor kept along X' X axis, carries a steady current I along the +x direction. At an instant t, a particle of mass m and charge q at point (x, y) moves with a velocity `vecv` along +y direction. Find the magnitude and direction of the force on the particle due to the conductor.
State the expression for the Lorentz force on a charge due to an electric field as well as a magnetic field. Hence discuss the magnetic force on a charged particle which is (i) moving parallel to the magnetic field and (ii) stationary.
State dimensions of magnetic field.
What is the relation between Tesla and Gauss?
A circular coil of wire is made up of 200 turns, each of radius 10 cm. If a current of 0.5A passes through it, what will be the Magnetic field at the centre of the coil?
