Advertisements
Advertisements
प्रश्न
Two long, straight, parallel conductors carry steady currents, I1 and I2, separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other? Obtain the expression for this force. Hence, define one ampere.
उत्तर
Magnetic field induction at some point P on wire 2 due to current I1 passing through wire 1 is given by
`B_1=(mu_0 2I_1)/(4pid)`
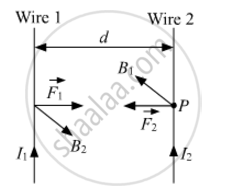
As the current-carrying wire 2 lies in magnetic field produced by wire 1, the unit length of wire 2 will experience a force, which is given by
`F=B_1I_2xx1=(mu_0)/(4pi) (2I_1I_2)/d`
According to Fleming's left-hand rule, the force on wire 2 acts in the plane of paper perpendicular to wire 2, directed towards wire 1. Similarly, wire 1 also experiences the same force towards wire 2.
Thus, both the conducting wires attract each other with the same force F.
Thus, one ampere can be defined as the amount of current flowing through two parallel conductors (in the same direction or opposite directions) placed at a distance of one metre in a free space, and both the wires attract or repel each other with a force of 2×10−7 Nm−1 per metre of their lengths.
संबंधित प्रश्न
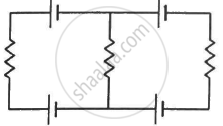
Each of the batteries shown in figure has an emf equal to 5 V. Show that the magnetic field B at the point P is zero for any set of values of the resistances.
According to the right-hand rule, the direction of magnetic induction if the current is directed in an anticlockwise direction is ______
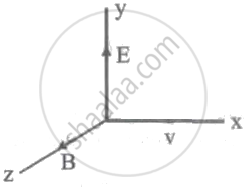
A particle with charge q moves with a velocity v in a direction perpendicular to the directions of uniform electric and magnetic fields, E and B respectively, which are mutually perpendicular to each other. Which one of the following gives the condition for which the particle moves undeflected in its original trajectory?
A very high magnetic field is applied to a stationary charge. Then the charge experiences ______.
Lorentz Force generally refers to ______.
In the product `vec"F" = "q" (vec"υ" xx vec"B")`
= `"q" vec"υ" xx ("B"hat"i" +"B"hat"j" + "B"_0hat"k")`
For q = 1 and `vec"υ" = 2hat"i" + 4hat"j" + 6hat"k"` and
`vec"F" = 4hat"i" - 20hat"j" + 12hat"k"`
What will be the complete expression for `vec"B"`?
A charged particle of charge e and mass m is moving in an electric field E and magnetic field B. Construct dimensionless quantities and quantities of dimension [T]–1.
An electron enters with a velocity v = v0i into a cubical region (faces parallel to coordinate planes) in which there are uniform electric and magnetic fields. The orbit of the electron is found to spiral down inside the cube in plane parallel to the x-y plane. Suggest a configuration of fields E and B that can lead to it.
A long straight conductor kept along X' X axis, carries a steady current I along the +x direction. At an instant t, a particle of mass m and charge q at point (x, y) moves with a velocity `vecv` along +y direction. Find the magnitude and direction of the force on the particle due to the conductor.
Distinguish between the forces experienced by a moving charge in a uniform electric field and in a uniform magnetic field. (Any two points)
