Advertisements
Advertisements
प्रश्न
According to the right-hand rule, the direction of magnetic induction if the current is directed in an anticlockwise direction is ______
पर्याय
perpendicular and inwards
perpendicular and outwards
same as current
opposite to that of current
उत्तर
According to the right-hand rule, the direction of magnetic induction if the current is directed in an anticlockwise direction is perpendicular and outwards.
संबंधित प्रश्न
(a) Write the expression for the magnetic force acting on a charged particle moving with velocity v in the presence of magnetic field B.
Two long, straight, parallel conductors carry steady currents, I1 and I2, separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other? Obtain the expression for this force. Hence, define one ampere.
Use this law to find magnetic field due to straight infinite current carrying wire.
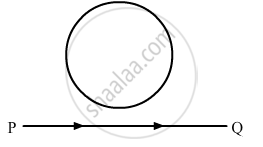
A conducting loop is held above a current carrying wire PQ as shown in the figure. Depict the direction of the current induced in the loop when the current in the wire PQ is constantly increasing.
A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire.
A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line?
A circular coil carrying a current I has radius R and number of turns N. If all the three, i.e. the current
I, radius R and number of turns N are doubled, then, the magnetic field at its centre becomes:
(a) Double
(b) Half
(c) Four times
(d) One fourth
A steady current (I1) flows through a long straight wire. Another wire carrying steady current (I2) in the same direction is kept close and parallel to the first wire. Show with the help of a diagram how the magnetic field due to the current I1 exerts a magnetic force on the second wire. Write the expression for this force.
The free electrons in a conducting wire are in constant thermal motion. If such a wire, carrying no current, is placed in a magnetic field, is there a magnetic force on each free electron? Is there a magnetic force on the wire?
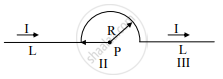
A conductor has three segments; two straights of length L and a semicircular with radius R. It carries a current I What is the magnetic field B at point P?
Show that currents in two long, straight, parallel wires exert forces on each other. Derive the expression for the force per unit length on each conductor.
A particle with charge q moves with a velocity v in a direction perpendicular to the directions of uniform electric and magnetic fields, E and B respectively, which are mutually perpendicular to each other. Which one of the following gives the condition for which the particle moves undeflected in its original trajectory?
A charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other. The particle will move in a ____________.
Direction of magnetic force on a positive charge moving in a magnetic field is given by ______.
Lorentz Force generally refers to ______.
Correct unit of magnetic field is ______.
The correct plot of the magnitude of magnetic field `vec"B"` vs distance r from centre of the wire is, if the radius of wire is R.
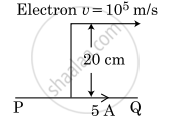
An infinitely long straight conductor carries a current of 5 A as shown. An electron is moving with a speed of 105 m/s parallel to the conductor. The perpendicular distance between the electron and the conductor is 20 cm at an instant. Calculate the magnitude of the force experienced by the electron at that instant.
A circular current loop of magnetic moment M is in an arbitrary orientation in an external magnetic field B. The work done to rotate the loop by 30° about an axis perpendicular to its plane is ______.
Consider a wire carrying a steady current, I placed in a uniform magnetic field B perpendicular to its length. Consider the charges inside the wire. It is known that magnetic forces do no work. This implies that ______.
- motion of charges inside the conductor is unaffected by B since they do not absorb energy.
- some charges inside the wire move to the surface as a result of B.
- if the wire moves under the influence of B, no work is done by the force.
- if the wire moves under the influence of B, no work is done by the magnetic force on the ions, assumed fixed within the wire.
A charged particle would continue to move with a constant velocity in a region wherein ______.
- E = 0, B ≠ 0.
- E ≠ 0, B ≠ 0.
- E ≠ 0, B = 0.
- E = 0, B = 0.
Show that a force that does no work must be a velocity dependent force.
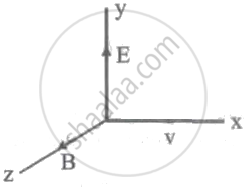
An electron enters with a velocity v = v0i into a cubical region (faces parallel to coordinate planes) in which there are uniform electric and magnetic fields. The orbit of the electron is found to spiral down inside the cube in plane parallel to the x-y plane. Suggest a configuration of fields E and B that can lead to it.
At a certain place the angle of dip is 30° and the horizontal component of earth’s magnetic field is 0.5 G. The earth’s total magnetic field (in G), at that certain place, is ______.
Two long current-carrying conductors are placed parallel to each other at a distance of 8 cm between them. The magnitude of the magnetic field produced at the mid-point between the two conductors due to the current flowing in them is 300µT. The equal current flowing in the two conductors is ______.
Write the expression for the Lorentz force on a particle of charge q moving with a velocity `vecv` in a magnetic field `vecB`. When is the magnitude of this force maximum? Show that no work is done by this force on the particle during its motion from point `vecr_1` to point `vecr_2`.
With a neat labelled diagram, explain cyclotron motion and cyclotron formula.
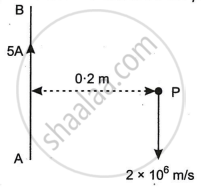
A long straight wire AB carries a current of 5A. P is a proton travelling with a velocity of 2 × 106 m/s, parallel to the wire, 0.2 m from it and in a direction opposite to the current, as shown in Figure below. Calculate the force which magnetic field of the current carrying conductor AB exerts on the proton.